안녕하세요. 이번시간에는 기존의 WinForm에서 사용하던 Clone메서드를 WPF에서는 어떻게 사용하는지에 대해 알아보도록 하겠습니다. WPF에서는 특별하게 Clone 메서드를 제공하고 있지 않기때문에 Clone 메서드를 직접 구현 해야 합니다. 프로젝트를 하다가 생각나서 구현해놨던건데 알려드리면 유용할것 같아 포스팅합니다..
저같은 경우는 방법이야 여러가지가 있겠지만, 저같은 경우는 간단하게 UIElement객체를 XAML로 Export하고 다시 해당 객체를 Import하는 방식으로 사용합니다. 생각보다 부하가 심할 수 도 있는 부분이긴하나, 간단하게 한두번 정도 사용하기에는 큰 무리는 없을 것으로 보입니다.
아래는 제가 사용하는 CloneElement 메서드 소스코드입니다.
- public static UIElement CloneElement(UIElement Source)
- {
- if (Source == null) return null;
- string XAML = System.Windows.Markup.XamlWriter.Save(Source);
- System.IO.StringReader StringReader = new System.IO.StringReader(XAML);
- System.Xml.XmlReader xmlReader = System.Xml.XmlTextReader.Create(StringReader);
- return (UIElement)System.Windows.Markup.XamlReader.Load(xmlReader);
- }
public static UIElement CloneElement(UIElement Source)
{
if (Source == null) return null;
string XAML = System.Windows.Markup.XamlWriter.Save(Source);
System.IO.StringReader StringReader = new System.IO.StringReader(XAML);
System.Xml.XmlReader xmlReader = System.Xml.XmlTextReader.Create(StringReader);
return (UIElement)System.Windows.Markup.XamlReader.Load(xmlReader);
}- Button OriginalButton = new Button();
- Button CloneButton = CloneElement(OriginalButton) as Button;
Button OriginalButton = new Button();
Button CloneButton = CloneElement(OriginalButton) as Button;.............
연달아 글 쓰는건 좀...
귀찮은듯??-ㅁ-a
이번 시간(?)은 사용자 에게서 입력을 받아서, 그 변수를 가지고 활용해 보도록 하겠습니다.
입력을 받는 방법은 이때 까지 출력으로 써왔던 SimpleDialog를 이용하시면 됩니다. 훗. -_-a
먼저 SimpleDialog와 Calculate Activity를 추가하여 줍니다.
그리고 그 둘을 연결 하여 줍니다. 그러면 다음과 같은 Connections 창이 뜹니다.

그러면 위와 같이 PromptDialog - Success를 선택하고 OK를 하여줍니다.

현재 까지 상태 입니다.
여기 까지 하셨으면 SimpleDialog를 하나 더 추가 하여 줍니다. 그러면 Add Activity라는 창이 하나 더 뜹니다.
현재 Diagram에 SimpleDialog가 있기 때문에 뜨는데, 원래 있는 SimpleDialog와 별반 다르지 않기 때문에 아래의 SimpleDialog를 선택하시고 OK를 눌러줍니다.

그리고 Calculate Activity 와 방금 추가한 SimpleDialog Activity를 연결합니다. 그러면 또 Connections 창이 뜨는데 AlertDialog를 선택하고,
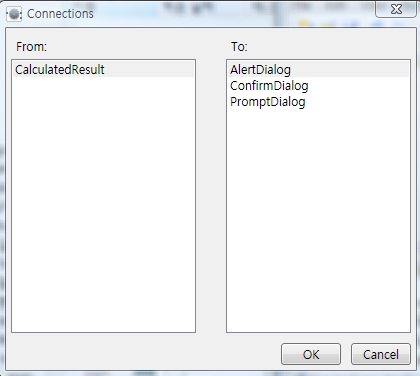
Value는 value를 선택하고 OK합니다.

다 하셨으면 다음과 같은 모습일 것입니다.

그러면 실행을 하여 주시면~~!
입력을 받을 Prompr Dialog창이 뜹니다.

그러면 입력 창에 원하는 문자열 아무거나 적으시고 OK를 클릭하시면~

위와 같이 적은 문자열이 그대로 출력이 됩니다.
지난 글과 연계하여 Calculate Activity 를 수정하여서, 또 다른 상태로 출력을 하여 보세요~
참 쉽죠~?
.............ㅜㅜㅜㅜㅜㅜ
..........
저번주 한번 날렸네요... -_-;;
시사회 간다고 바쁘게 그날 하루 날려 주시고~
이번주에 두개 올라 갑니다~~!
VPL 기본 1 에서는 Hello World! 를 출력 하는 것을 해보았습니다.
그냥 단순히 변수 값 만 날리는거 말고, 변수 값을 받아서 처리 하여 출력하여 보도록 하겠습니다.
저번의 Hello World! 하는 것에서 약간 변형을 해서 Variable과 Calculate 라는 Activity를 하나 씩 추가 해 줍니다.

그러면 위와 같은 상태가 됩니다.
Data 에 string형 변수로 "홍길동"을 넣어주면 "당신은 홍길동 입니다" 로 메세지를 출력 해 보도록 하겠습니다.
그러면 Data에 string형으로 변환하여 홍길동을 적어주시고, Variable 에는 your name으로 지정해줍니다.

위와 같이 하시면 되는데 Data와 Variable을 연결 하시면 다음과 같은 창이 뜨는데 거기서 SetValue를 선택하시고 OK누르시면 됩니다.

그리고 Variable Activity에서 오른쪽 아래의 ... 라는 추가 버튼을 누르시면 다음과 같은 창이 뜹니다.

여기에서는 Add 버튼을 누르신 후 yourname이라는 변수로 설정해 줍니다. 물론 데이터 형은 string으로 하여야 겠죠.

그리고 Calculate에서는 yourname이라는 변수를 선택하여 주면 됩니다.

현재 까지 하셨으면 위와 같은 상태일꺼고 simpleDialog랑 Calculate를 연결 하시면 됩니다. 여기서는 지난 글의 방법과 같이 AlertDialog를 선택 하시면 되구요.

그 다음에 Data Connections 창이 뜨는데 거기선 value에서 value를 선택하시고 ok하시면 됩니다.


이 상태에서 실행을 하시면 변수를 처리 하지 않은 변수 상태 그대로 홍길동 이 출력이 됩니다.

변수 처리를 할려면~!! Calculate Activity에서 수정을 해 주어야 합니다.
string은 " " 로 닫아주시고, 그담에 + 하시면 두 변수 사이가 더해지는(??)구조?-ㅁ-a;;;; 다음의 그림과 같이 Calculate Activity를 수정하여 주시고 실행하시면.

다음과 같이 원하는 모습대로 출력이 됩니다.

뭐 이거 날로 먹는 느낌도 강하긴 한데.. 기초라 뭐 설명을 어찌.. 흡...-_-a
안녕하세요. 한주동안 잘지내셨는지요?^ ^;
오늘은 Hello World를 출력하는(?) 화면을 만들어 볼 생각입니다. ^ ^
모든 Programming 언어의 책의 첫장을 보면 화면에 Hello World를 띄우는 것부터 연습를 하죠? ^ ^; 그래서 저도 오늘은 Hello World를 화면에 보여주려고 합니다. 가장 기초적인 부분부터 뼈대를 만들어 가볼까요? ㅋㅋㅋ
이번에는 Source를 분석할때는 시그널(이벤트) 함수와 시그널 핸들러 함수에 대해서 집중적으로 설명해 볼까 합니다.
1. Hello World를 들어가기에 앞서..
이번에는 여태까지 내용과는 달리 중요한 부분이 몇가지 나오는 것 같아요. 중요한 부분이라면, gtk프로그래밍에서 interface를 다루는 부분이죠. interface란 사용자와 컴퓨터(or 윈도우) 사이의 관계를 말하며, 사용자가 요구하는 대로 반응하는 환경을 구현하는 것이 interface 프로그래밍이라고 합니다.
어떤 식으로 Hello World를 출력해 볼까요? 일단, 버튼과 label을 하나 만들어 볼까해요~ 버튼을 누르면 label의 내용이 "Hello World Open"으로 바뀌었다가 다시 한번 더 누르면 "Hello World Closed"로 바꾸도록 만들어 보겠습니다. 그럼 여기서도 알 수 있듯이 오늘은 버튼을 누름에 따라 변화를 구현하는부분이 핵심이라는 것을 알 수 있죠?
2. Hello World
#include <gtk/gtk.h>
GtkWidget *label;
void button_clicked ( gtkwidget *widget, gpointer data)
{
static int toggle = 1;
if (toggle == 1)
{
gtk_label_set_text ( gtk_label(label) , "hello world opened");
toggle = 0;
}
else
{
gtk_label_set_text ( gtk_label(label) , "hello world closed");
toggle = 1;
}
}
void delete_event ( gtkwidget *widget, gdkevent *event, gpointer data)
{
gtk_main_quit ();
}
int main( int argc,char *argv[] )
{
gtkwidget *window, *button;
gtkwidget *vbox;
gtk_init (&argc, &argv);
window = gtk_window_new (gtk_window_toplevel);
gtk_window_set_title(gtk_window (window), "upgrade hello world");
gtk_signal_connect ( gtk_object(window), "delete_event",
gtk_signal_func ( delete_event), null);
gtk_container_set_border_width ( gtk_container ( window), 10 );
vbox = gtk_vbox_new ( false,0);
gtk_container_add ( gtk_container ( window ), vbox);
label = gtk_label_new ("hello world closed");
gtk_box_pack_start (gtk_box(vbox), label, true, true, 0);
gtk_widget_show ( label);
button = gtk_button_new_with_label ("Click");
gtk_signal_connect ( gtk_object (button), "clicked");
gtk_signal_func ( button_clicked ), null);
gtk_box_pack_start (gtk_box(vbox), button, true, true, 0);
gtk_widget_show (button);
gtk_widget_show (vbox);
gtk_widget_show (window);
gtk_main ();
return(0);
}
3. Hello World Source 설명
main()을 보면 보지못했던 새로운 함수들이 보이죠?
gtk_window_set_title();
gtk_signal_connect();
gtk_container_set_border_width();
gtk_vbox_new();
gtk_button_new_with_label();
gtk_box_pack_start();
gtk_window_set_title();
위의 함수는 메인 윈도우의 제목을 정해 주는 부분입니다. title!! 이 글자만 봐도 대충 감이 잡히죠? ^ ^;
gtk_container_set_border_width();
이 함수는 window 의 border 의 크기를 정의합니다.
gtk_vbox_new();
gtk에서 윈도우 안의 여러가지 위젯들을 배열하기 위해서 box라는 위젯을 많이 씁니다. gtk는 window 안에 window를 삽입 할 수 가 없어서 이러한 도구를 앞으로도 많이 사용할 것입니다. table과 frame이 주로 사용되는 도구들 중의 하나이죠 ^ ^
box는 실제로 보여지는 위젯은 아니지만 다른 widget들을 배열하기 위해 사용하지요. box인데 vbox라고 사용한 것에 대해 의심이 가지 않아요? box는 두가지 종류가 있습니다. vbox와 hbox가 사용됩니다. 이것은 수직박스와 수평박스를 나타내지요. 물론 gtk_*_new()으로 정의할 수 있습니다. hbox와 vbox의 조합으로 위젯의 위치를 정해서 좀더 직관화된 인터페이스를 만들 수 있죠.
위의 "Hello World" source는 vbox를 정의하고 그곳에 레이블과 버튼을 올려놓습니다(packing). packing이라는 말은 widget들을 쌓아 넣는다고 보면됩니다. 예를들어 커다란 여행 가방에 여러가지 물품들을 차곡차곡 정리해야 한다면 vbox로 나눈뒤 수직 방향의 박스에 차곡차곡 widget을 넣어서 보기좋게 정돈되는 과정이라고 생각하시면 되죠 ^ ^ 머리속으로 그림을 그리면 좀더 쉽게 이해가 되실 겁니다.
gtk_button_new_with_label();
button을 정의하는데 label을 넣고 싶을 때 쓰는 함수입니다. 버튼에는 일반적으로 label이 보여서 사용자에게 어떤 역할을 하는지 알려주는 역할을 하죠.
gtk_box_pack_start();
gtk_container_add와 비슷한데.(기억나시죠? container에 무언가 추가하는^ ^;) 여기서는 박스에 쌓기(packing) 위해서 위 함수를 쓴다. gtk_box_pack_start()는 hbox 위젯의 왼쪽에서 오른쪽, vbox부분에서는 위쪽에서 아래쪽의 순으로 쌓는다는 의미이며, 반대 역할을 하는 gtk_box_pack_end()함수도 있습니다. 뒤에 붙는 인자들은 expand, fill할 것인가에 대한 선택이며, 마지막이 padding의 크기를 정의합니다.
이제부터.. 가장 중요한 부분을 설명해 보겠습니다. 제가 처음에 말씀드렸죠. 오늘은 가~장 중요한 무언가가 나올것이라구요.
이제 나타날 때가 되었습니다. 짜~~~잔!!!^ ^*
gtk_signal_connect( gtkobject *object,
gchar *name,
gtksignalfunc func,
gpointer func_data
);
위 함수는 interface , 즉 사용자가 뭔가를 행하였을(signal) 때 반응 하는 함수에 대해서 연결 (connect ) 시켜주는 역할을 합니다.
위의 예제(Hello World)중에서..
gtk_signal_connect ( gtk_object (button),
"clicked",
gtk_signal_func ( button_clicked ),
null);
예로 들자면, 사용자가 button이라는 위젯을 눌렀(click)을 경우 'clicked' 라는 이벤트가 발생하며, button_clicked라는 함수를 불러 실행하라는 의미가 됩니다. 실제 button_clicked는 소스의 윗부분에 정의하였습니다.
두 번째 인수인 "clicked"는 임의로 정해지는 것이 아닙니다. 이것은 각각의 위젯에 대해서 사용자가 행한 행동 (event라고도 할수 있다)을 말하며, 버튼이라면 누르는 것이 있을 것이며, 메뉴에서는 선택하는 부분등이 예가 될 수 있습니다. 이 event는 각각의 위젯에 따라 다르며, 그 이름또한 틀립니다. 그 이름은 미리 정의되어 있습니다. 물론 사용자가 임의의 위젯을 만들고 임의의 이벤트를 만들수는 있지만, 그것은 좀더 고차원적인 기술이기에 다음 기회에 해보아야겠습니다.
사용자가 버튼을 눌렀더니, button_clicked이라는 함수가 불러집니다. 실제 위 소스에서는 버튼이 눌러지면 label 의 내용을 토글시키는 작용을 하게 해놓았습니다. c 프로그래밍을 접한 우리들은 쉽게 접근할 수 있겠죠. 여기에서 마지막 인수는 함수에 넘겨질 데이터입니다. 이 데이터는 대부분 프로그래밍에서는 null이지만 사용자가 필요에 의해 임의의 값을 넘겨주어야 할 때 적어주면 됩니다.
위에 또다른 gtk_signal_connect가 있죠? 'delete_event' 이며 이는 시스템 버튼 (오른쪽 위의 x모양의 버튼) 이 눌러졌을 경우 gtk 내부에 미리 정의된 기본 함수, gtk_main_quit을 부르게 되어 있습니다. 단순히 윈도우를 종료시키는 함수죠. 사용자가 만들지 않아도 되는 (일반적인 이벤트 함수) 함수들은 미리 정의된 것들을 쓰기도 합니다.
그럼. 정리를 해볼까요? ^ ^;
(1) 우선 window을 생성하고, 박스를 만듭니다.
(2) label을 생성하고 초기 이름은 'hello world closed'이고 이것을 박스에 쌓아봅니다(packing).
(3) button을 만들고 초기 label은 '클릭해 주세요'이며, 버튼이 눌러질 경우 행하여질 이벤트 함수를 'button_clicked'라고 정의하였고 이벤트와 연결하였습니다. 버튼 또한 box에 packing시킵니다.
(4) 각각의 위젯을 보이게 합니다.
4. 결과 화면

오늘 저의 설명은 어떠하였는지요? ^ ^; 궁금한 사항이 있으면 댓글을 달아주세요 ^ ^
무언가 하나씩 해나아가는 듯한 느낌이 들지 않아요? ㅋㅋ 오늘은 무언가 설명 좀 한것 같아서 나름 뿌듯한걸요? ^ ^;
함수를 좀더 쉽게 설명하기 위해 책과 블로그들을 참고하였는데, 아직 많이 미흡-_-+ 이쁘게 봐주세요 ^ ^
GCC는 (GNU Compiler Collection)의 약자이다. GNU C Compiler라고 부르기도 하는데 GCC가 C++, JAva, Fortran, Ada등 많은 프로그래밍 언어를 지원하면서 부터 단순히 C Compiler라고 부르기보다는 전자의 경우가 맞을 것이라 생각한다.
GCC의 가장 큰 장점은 현존하는 수많은 Architecture의 지원이다. x86부터 시작하여 ARM, MIPS, PowerPC, Sparc등등 현존하는 대부분의 아키텍쳐를 지원한다. 이렇게 많은 아키텍쳐를 지원할 수 있었던 것은 각 아키텍쳐로의 포팅이 용이하게 구성되어져 있기 때문이다. 따라서 새로운 아키텍쳐를 GCC에 포팅하는 일도 간단하지는 않겠지만 새로운 컴파일러를 제작하는것에 비해 상당한 수고를 덜 수 있을 것이다.
그럼 간단히 GCC의 컴파일 과정을 알아보자.
소스파일(.c) ->> 전처리후 파일(.i) ->> 어셈블리 파일(.s) ->> 오브젝트 파일 (.o) ->> 최종 실행파일(ELF)
(전처리과정) (컴파일과정) (어셈블러과정) (링킹과정)
이것이 보통 gcc가 컴파일 되는 과정이다.
gcc로 보통 -o 옵션을 주게 되면 각 단계별로 생성되는 파일을 최종 ELF실행을 만들어 낸후 다 삭제 해 버린다. 중간 생성 파일들을 보기위해서는
gcc -E 옵션을 주면 .i파일을 볼 수 있고 -S 옵션을 주면 .s파일을 생성하며, -c 옵션을 주면 .o파일을 만들어내게 된다. 이것 모두를 다 보고 싶다면 --save-temps 옵션을 주게 되면 중간생성 파일들을 보두 볼 수 있다.
컴파일러는 단순히 고레벨 수준의 언어를 최종 아키텍쳐의 목적코드로 만들어내는데에 그 역할이 있지 않다. 현대 컴파일러에서 가장 중요한 부분은 최적화 부분이다. 사용자가 작성한 코드가 해당 아키텍쳐에서 최적으로 동작하게끔 목적코드를 생성해 주어야 한다. 그래야 프로그램의 성능을 극대화 시킬 수 있다. 그 과정이 .i 에서 .s로의 컴파일과정에 일어나게 된다.
이과정은 크게 4가지로 나뉘어 지는데
GENERIC tree -> GIMPLE tree -> SSA -> RTL
이런순서대로 GCC는 해당 소스파일을 여러단계에 걸쳐 최적화를 이루어내게 된다.
크게 최적화는 두가지 부류로 나누어 볼 수 있는데 컴퓨터 아키텍쳐에 종속적인 최적화와 그렇지 않은 최적화로 나누어 볼 수 있다. RTL전 까지는 아키텍쳐에 비종속적인 최적화가 일어나고 RTL변환후에는 아키텍쳐 종속적인 최적화가 이루어지게 된다.
보통 학부 컴파일러 과정에서는 파싱(토큰, 문법체크)과 의미분석(타입체크 등등)과정까지만 배우고 만다. 이런 부분을 front-end라고 부르고 그 뒤의 최적화 부분을 back-end라고 부른다. front-end는 이미 많은 해결책과 거의 최적화된 솔루션이 존재해 현재 연구분야에서는 거의 제외되고 있다고들 하고, 최적화 부분인 back-end가 주요 관심사라고 한다.( 생각해보면 컴퓨터 아키텍쳐의 발전에 따라 계속 고려되어야 하는 부분이니 계속 연구의 수요는 일어날 것이라 생각된다. )
여튼 학부과정에서 배운 파싱과정을 거쳐 파싱트리가 만들어지면 이것을 프로그래밍 언어에 독립적인 general한 트리로 만들게 된다. 이것이 바로 GENERIC 트리이다. 이후에 아키텍쳐 비종속적인 최적화를 이루기 위해 트리를 좀더 변경시키는데 이것이 GIMPLE 트리에 해당한다. GIMPLE 트리에서 한단계 더 변형을 가하는데 이것이 바로 SSA(Static Single Assignment)형태이다.
이렇게 아키텍쳐 비종속적인 최적화를 수행한후에 거의 어셈블리 형태와 유사한 RTL( Register Transfer Language)로 변환한후 여기서 아키텍쳐 종속적인 최적화를 수행하게 된다. ->각 트리에 대한 얘기는 추후에....
|
오실로스코프의 대역폭
|
1. 오실로스코프 아날로그 대역폭(Analog Bandwidth)은 입력되는 정현파의 진폭이 -3dB
(대략 30%) 저하되는 지점의 주파수로 정의 합니다.

2. 오실로스코프의 대역폭별 50 MHz 구형파 신호의 재생

3. 구형파나 펄스파와 같이 빠른 상승 또는 하강 시간을 갖는 신호를 측정시 다량의 고주파
성분을 포함하고 있어 신호의 반복 주기만을 감안한 스코프 대역폭 선택은 의미가 없을 수
있습니다. 따라서, 신호의 주파수 보다 높은 대역폭을 갖는 스코프를 사용하여야 합니다.
* 오실로스코프의 신호대비 낮은 대역폭으로 인한 영향
- 신호의 상승/하강 시간이 길어진다.
- 신호의 진폭을 감소 시킨다.
* 오실로스코프의 대역폭 계산법
암튼 이번 블로깅의 주제는 제 졸작이구요. 한 2~3편에 걸쳐서 올려볼까 합니다. 디자인 전시회지만 나름 '디자인+소프트웨어+하드웨어' 가 하나된 대형 프로젝트라 ...누군가 그러더군요...;;; 이런저런것 많이 보시다 보면 분명 개발하시는데 아이디어 짜시는데도 많은 도움이 될꺼라 믿어 의심치 않습니다! 라는 생각에서 이러한 내용으로 블로깅을 해봅니다. 시그장님 괜찮죠?
그럼 들어갑니다!
free your mind #1
방식에서 차이점을 주고자 목표한 프로젝트이다.
방식은 간단하다. :) 사용자는 앞에놓인 버튼을 사운드에 맞춰 자신만의 느낌으로 눌러본다.
눈앞에는 다양한 영상이 펼쳐진다. 즉 다시말해서 사용자는 음악을 양념삼아 버튼을 누르는것
만으로 영상을 제작한다. 일종의 '놀이' 개념으로 다가가고자 하였다.
다음은 작품 프리젠테이션...











초기에는 브랜딩을 배제하고 작품 그자체로 의미를 두려고 하였으나 교수님과의 면담을 통해서
MTV라는 브랜딩을 하기로 결정되었다. 대학생이라는 나름의 '타이틀'을 걸고 아트와 디자인사이에서
줄타기를 시도하려 했었던 건방진(?) 생각은 결국 교수님과의 타협으로 끝나고 만 것이다.
하지만 작품의 순수의도는 절대 변하지 않는다. 다양한 음악을 다양한 시각으로 해석 할 수 있도록
할 것이며, 사용자가 이 작품을 통해 흥을 돋굴수 있다면 그것만으로도 충분히 승산이 있다고 생각한다.
이번시간에는 포인트 연산 중 두 프레임간의 산술연산에 대해 포스팅하겠습니다.
많이 어려운 내용은 아니지만, 실제로 많이 사용되는 기본중 기본이라고 하니 자세히 알아두는게 좋겟습니다-
구현된 결과는 파일로 첨부 해 봅니다.
(글을 수정하면 동영상도 올려보도록 하겠습니다.
아직까지 만족할만한 예쁜동영상이 안나와서 ㄷㄷㄷ)
픽셀단위의 산술연산을 할 경우는 상수에 의한 연산과 마찬가지로 ..
기본 산술연산에 있는 네가지 + (덧셈) - (뺄셈) * (곱셈) / (나눗셈) 가 있습니다.
간단하게 말하자면 산술연산시 상수값을 더하거나 빼는 것처럼
같은 위치의 픽셀의 밝기 값에 같은 위치의 픽셀의 밝기를 더하거나 빼서
새로운 영상을 만드는 처리방법입니다.
서로다른 두 영상의 합(SUM)

원숭이와 동그라미 영상의 합

레나와 원 영상의 합
서로 다른 두 영상내에서 각각의 대응 픽셀의 밝기 값을 합해서 나온 결과 영상입니다.
물론 합한후의 픽셀의 밝기 값이 255를 초과하는 경우 255의 값을 가지게한 saturation기법을 사용하였습니다.
이를 통하여 원하는 부분의 그림만을 추출할 수 있도록 할 수 있어. 이미지 추출에 많이 사용된다고 합니다.
서로 다른 두 연산의 차 (SUB)

빼기연산을 이용한 불량검사

빼기연산을 이용한 불량검사2

빼기연산을 이용한 움직임 검출
실제로 많이 사용한다고 하는 빼기연산의 예들입니다.
처음과 두번째 그림처럼 어떠한 물체의 결함을 찾기 위해서 많이 사용된다고 합니다.
또한 침입자 검출을 위하여 다음과 같은 연산을 하여도 침입자가 발생하엿다는 사실을 쉽게 알 수 있습니다.
하지만, 이러한 빼기 연산을 통하여 결함을 찾거나, 침입자를 검출하기 위해서는, 촬영하는 카메라의 이동이 없어야 하는것!.
만약 카메라 자체의 이동이 있다면 빼기연산을 하여도 결과가 무지 이상하게 나옵니다. -_-;;;
(적당한 이미지를 찾지못해서 이미지 첨부는.. 수정으로 미루겠습니다. ㅠ)
곱하기, 나누기 연산-_-ㅋ
물론 상수를 이용한 산술연산처럼 두 이미지에서도 곱하기 나누기 연산을 사용할 수 있습니다.
위의 이미지를 사용하여 나온 결과는 이러합니다...

두 이미지 같의 곱셈연산

두 이미지 간의 나눗셈연산
만..
적당히,, 좋은 예의 이미지를 찾지 못하였기 때문에,, 구현결과는 다음과 같습니다..
(사실 이 연산들을 어디에 사용해야할 지 잘 모르겠습니다.. ㅠㅠ)
추후에 어디에 사용되는 연산인고-_-; 를 알게되면 이 내용을 초금 수정할 예정.....입니다..
p.s 앗 한가지 신기한것

두 프래임간의 덧셈 연산인데,
이를 통하여 손을 거쳐서 뒷모습이 보이는 모습을 볼 수 있지 않은가요??ㅋ
... 저만 신기하다면 쿨럭..;;;
구현된 내용의 소스는 이러합니다.
어렵지 않아서 쉽게 이해하 실 수 있으실 겁니다.
안녕하세요.
오늘은 바이너리서치(Binary Search) 의 코딩법에 대해서 알아보겠습니다.
숫자맞추기
참이슬을 까고나면 병뚜껑을 꼬은 다음에 손가락으로 쳐서 끊어지면 그 전사람이 벌주를 마시는 게임이 있죠?? 그리고 나서 벌주를 마신 사람은 병뚜껑에 있는 숫자를 보고 업&다운을 해서 그 숫자를 부른 사람이 또 벌주를 마십니다. (이거 우리 학교만 하나요?)
혹시나 모르시는 분이 있을까봐 부가 설명을 드리겠습니다.
참이슬 병뚜껑에는 [1, 50] 사이의 숫자가 찍혀있습니다. 한사람씩 숫자를 부르면 정답을 아는 사람이 정답에 지금 부른 숫자보다 큰지 작은지를 알려줍니다. 그 다음 사람은 좁혀진 범위 내에서 숫자를 다시 부릅니다. 그럼 범위가 점점 좁혀지고 누군가 숫자를 맞추게 되는데 그 사람이 벌주를 마시게 됩니다.
이 게임을 하고 있는 모든 사람이 화장실을 가고 싶어서 최대한 게임을 빨리 끝내기위해 최선을 다한다면 최대 몇 번째 사람까지 턴이 돌아갈까요??
그렇습니다. 정답은 6회입니다. 확인을 위해 검증을 해보도록 하겠습니다.
2회: [26, 50] - 38을 부름 [26, 37], [39, 50] 모두 12개의 숫자가 남아있으므로 어떤 범위가 남아도 최소횟수는 같음
3회: [26, 37] - 31을 부름 [26, 30], [32, 37] 중 [32, 37]이 숫자가 하나 더 많으므로 최악의 경우는 [32, 37]
4회: [32, 37] - 35를 부름 [32, 34], [36, 37] 중 [32, 34]가 숫자가 하나 더 많으므로 최악의 경우는 [32, 34]
5회: [32, 34] - 33을 부름 [32, 32], [34, 34] 모두 하나만 남았음
6회: 하나만 남았습니다. 번호를 부르고 소주를 원샷하세요
모든 사람이 최선을 다 했을때 숫자가 하나가 남을때까지 게임이 지속된 예를 들었는데요. 이를 수식화 하여 풀 수 있습니다.
한 턴이 지날때 마다 숫자의 범위가 반씩 줄어들게 됩니다. n번째 턴에서 남은 숫자의 범위를 T(n)이라 하면,
T(n) = ceiling[ 0.5 * T(n-1) ] , ceiling은 올림입니다.
이 되고 식을 마스터정리(Master theorem)을 이용하여 풀면
T(n) = O(lg n) 이 됩니다. (여기서 lg는 밑이 2인 로그입니다)
아까 소주게임에 적용해 보면 n이 50 이므로 ceiling[ lg 50 ] = 6 이 되는것을 확인할 수 있습니다.
이처럼 바이너리서치를 적용하면 한 턴이 지날때마나 남아있는 후보의 범위를 반으로 팍팍 줄여나가기 때문에 검색을 해야하는 경우 아주 강력한 도구가 될 수 있습니다.
생각보다 어려운 바이너리서치
Knuth는 <Sorting and Searching>에서 이진탐색이 처음 발표된 것은 1946년이고, 버그가 없는 최초의 이진탐색 코드는 1962년이 되어서야 나타났다고 지적했습니다. 버그프리한 바이너리서치루틴도 보면 정말 간단합니다. 왜 이렇게 간단한걸 작성하는데 20년이나 걸렸는지 생각해 보면 그 만큼 버그없는 프로그램을 만든다는 것이 어려운 일이고 tricky한 버그를 발견하기도 쉬운일이 아닌가 봅니다.
아래의 의사코드를 봅시다.
INT U = N // 상한
INT Solution = -1 // 원하는 결과가 있는 위치 (-1: 원하는 결과를 찾을 수 없음)
// 하한이 상한보다 같거나 작으면 반복
Repeat Until (L <= U)
Begin Repeat
// 원하는 결과를 찾음
If (find solution at T) Then
Break
// T에 대한 값이 원하는 값보다 큰 경우 -> 상한을 T보다 1 작은 값으로 변경
If (value at T is greator than solution) Then
// T에 대한 값이 원하는 값보다 작은 경우 -> 하한을 T보다 1 큰 값으로 변경
If (value at T is less than solution) Then
Return Solution
구현1 - 배열에서 원소 검색(반복적 방법)
원소가 비내림차순으로 정렬된 배열에서 바이너리서치 - 반복적 방법
- // 원소가 비내림차순으로 정렬이 되어 있는
- // 크기 n의 배열 Array에서 key가 저장되어 있는 위치를
- // 바이너리서치를 이용하여 리턴
- // key가 없는 경우 -1을 리턴
- int BinarySearchLoop(int Array[], int n, int key)
- {
- int U = n-1;
- int L = 0;
- while (L <= U) {
- int T = (U + L) / 2;
- if (Array[T] == key) return T;
- if (Array[T] > key) U = T - 1;
- else L = T + 1;
- }
- return -1;
- }
구현 2 - 배열에서 원소 검색(재귀적 방법)
원소가 비내림차순으로 정렬된 배열에서 바이너리서치 - 재귀적 방법
- // 원소가 비내림차순으로 정렬이 되어 있는
- // 배열 Array에서 key가 저장되어 있는 위치를
- // 바이너리서치를 이용하여 리턴
- // key가 없는 경우 -1을 리턴
- int BinarySearchRecursive(int Array[], int L, int U, int key)
- {
- if (L > U) return -1;
- int T = (U + L) / 2;
- if (Array[T] == key) return T;
- if (Array[T] < key) return BinarySearchRecursive(Array, L, T-1, key);
- else return BinarySearchRecursive(Array, T+1, H, key);
- }
실수범위에서의 바이너리서치
위에서 정수를 기준으로 바이너리 서치를 하는 방법을 반복적 방법과 재귀적 방법으로 살펴보았는데요 상황에 따라서는 실수범위에 대해서 바이너리서치를 해야할 경우도 발생합니다. 뉴턴메소드(Newton's Method)가 그 예인데요 실수 범위에서 바이너리서치를 하는 경우에는 대체로 오차범위가 주어지고 그 오차범위내에 탐색범위가 들어갈때까지 반복을 하게됩니다.
반복적 방법이든 재귀적 방법이든 바이너리서치를 진행하면서 한 이터레이션이 지날때마다 탐색범위가 반으로 줄어들는 것을 이용하는 겁니다.
예를 들어 오차범위 1e-9 이내에서 답을 구하고 싶으면 low bound와 upper bound의 차이가 1e-9 보다 작아질때까지 반복을 하면 됩니다. 제가 개인적으로 더 추천하는 방법은 그냥 충분히 많이 이터레이션을 하는 것입니다. 무슨말이냐 하면 한 100번 정도 무조건 반복을 하는 겁니다.
이게 지금 무슨말을 하는 거냐!! 라고 생각할 수도 있는데요.. 바이너리서치의 이터레이션을 100번을 반복하면 탑색범위가 1/(2^100)까지 좁혀지게 됩니다. 이 정도 탑색범위라면 1e-9 이내로 들어가지 않을까요?? 뭐 상황에 따라 적잘하게 이터레이션 횐수를 정해주면 됩니다만 제 생각엔 최악의 경우에도 1000번 정도면 충분할것이라 생각합니다.
그렇다면 오차범위 내에 들어갈때까지만 비교하면 될것을 왜 쓸데없이 반복을 하냐라고 물어볼수도 있는데요.. 제가 적당히 큰 횟수만큼 반복하는 것을 권장하는 이유는 오차범위 비교 방법은 실수연산의 특성상(precision error가 생기죠) 오차범위내로 수렴하지 못해 무한루프에 빠질 가능성이 있기 때문입니다.
아래에서 3차 방정식의 해를 바이너리서치를 이용하여 구하는 예를 보겠습니다.
구현 3 - ax^3 + bx^2 + cx + d = 0 의 해를 구함(허용 오차범위 1e-9) - 실수범위 바이너리서치(오차범위)
- // ax^3 + bx^2 + cx + d = 0 의 해를 구합니다.
- // 해는 [-1000000000, 1000000000]에 존재한다고 가정함
- double EPSILON = 1e-9;
- double CubicFunction1(double a, double b, double c, double d)
- {
- double L = -1000000000;
- double U = 1000000000;
- double T = (L + U) / 2;
- while (U - L >= EPSILON) {
- double y = a*T*T*T + b*T*T + c*T + d;
- if (y > 0) U = T;
- else L = T;
- T = (L + U) / 2;
- }
- return T;
- }
구현 4 - ax^3 + bx^2 + cx + d = 0 의 해를 구함(허용 오차범위 1e-9) - 실수범위 바이너리서치(적당히반복)
- // ax^3 + bx^2 + cx + d = 0 의 해를 구합니다.
- // 해는 [-1000000000, 1000000000]에 존재한다고 가정함
- double CubicFunction2(double a, double b, double c, double d)
- {
- double L = -1000000000;
- double U = 1000000000;
- double T = (L + U) / 2;
- for (int i = 0; i < 100; i++) {
- double y = a*T*T*T + b*T*T + c*T + d;
- if (y > 0) U = T;
- else L = T;
- T = (L + U) / 2;
- }
- return T;
- }
문제를 풀어봅시다.
이론만 늘어서는 소용이 없겠죠?? 아는 것을 실전에 써 먹을 수 있는 준비가 되어있어야 진정 내것이라고 말할 수 있습니다.
우리같이 아래 문제를 풀어보아요
직선상에 N개의 행성들이 위치해 있습니다. i 번째 행성은 x[i] 좌표에 있고, m[i] 만큼의 질량을 가지고 있으며, 각각의 행성들은 매우 강한 힘에 의하여 고정되어 있습니다. 모든 행성은 x좌표를 기준으로 비내림차순으로 정렬되어 주어집니다.
질량이 m1, m2인 두 물체 사이의 거리가 d일 때, 두 물체는 서로 F = G * m1 * m2 / d^2 의 힘으로 서로 잡아당기는 만유인력이 작용합니다. (G는 양의 상수이다.) 어떤점 P를 기준으로 만유인력의 벡터합이 0이 되는 P의 위치를 equilibrium Point라고 부릅니다.
N개의 점이 있을 때, N-1개의 Equilibrium Point가 존재합니다. 이러한 Equilibrium Point들을 오름차순으로 정렬하여 소수점이하 9자리까지 출력하시오.
힌트: 각 Equilibrium Point는 이웃한 행성과 행성사이에 하나씩 존재합니다.
풀이보기
EP의 위치를 x'이라 하고 가상의 질량 m'을 부여하면 EP의 왼쪽에 위치한 행성으로부터 받는 중력은 다음과 같습니다.
EP는 중력이 0이 되는 위치이므로 양쪽에서 받는 중력이 같아야 합니다. 따라서 F1 = F2인 x'을 찾아야합니다.
G * m' * ∑ m[k] / (x[i] - x')^2 (k = 0....i) = G * m' * ∑ m[k] / (x[i] - x')^2 (k = i+1....n)
양변의 G * m' 을 소거하면,
∑ m[k] / (x[i] - x')^2 (k = 0....i) = ∑ m[k] / (x[i] - x')^2 (k = i+1....n)
m과 x는 주어지므로 위 식에서 미지항은 x'밖에 없습니다. x'은 뉴턴메소드(바이너리서치)를 이용하여 구할 수 있습니다.
- void EquilibriumPoint(double x[], double m[], int n)
- {
- // n-1개의 Equilibrium Point가 존재함
- for (int i = 0; i < n-1; i++) {
- double L = x[i];
- double U = x[i+1];
- double T = (L + U) / 2;
- // 적당히 큰 횟수 반복(200회 -> 오차범위 1/(2^200))
- for (int j = 0; j < 200; j++) {
- double F1 = 0;
- double F2 = 0;
- // 왼쪽에 위치한 행성의 중력의 합
- for (int k = 0; k <= i; k++)
- F1 += m[k] / pow(x[k] - T, 2.0);
- // 오른쪽에 위치한 행성의 중력의 합
- for (int k = i+1; k < n; k++)
- F2 += m[k] / pow(x[k] - T, 2.0);
- // 왼쪽에서 더 큰 중력을 받음 -> EP는 좀 더 오른쪽에 있다
- if (F1 > F2)
- L = T;
- // 오른쪽에서 더 큰 중력을 받음 -> EP는 좀 더 왼쪽에 있다.
- else
- U = T;
- T = (L + U) / 2;
- }
- printf("%.9f\n", T);
- }
- }
출처: TopCoder - Single Round Match 421
휴.. 이상으로 바이너리서치에 대해서 알아봤는데요.. 왠지 쓰고나니 마지막 문제가 좀 어려웠던게 아닌가 생각이 드네요 ^^;;
다음에는 주제를 약간 벗어나서 C++의 STL(Standard Template Library)에 대해서 포스팅을 해볼까 합니다.
뭐 제가 C++을 주로 사용하다 보니.. C++을 안쓰시는 분들한테는 전혀 도움이 되지 않겠지만 그래도 알아두면 좋겠지요 ㅎㅎ
이전글 [UNIX 보안 기초 -3-] 대표적인 해킹유형
벌써 한주가 지나갔습니다. 시간 참 빠르네요. 다들 중간고사도 끝났겠구..이제 새로운 시작을 해봅시다. 저는 매번 시작인것 같네요..ㅠ
이번부터는 몇가지 해킹 기법에 대해 약간 깊숙히 소개하려 합니다. 오늘은 BOF(Buffer Over Flow 공격) 인데요. 얼마전 구글폰 G1 과 구글 웹브라우저 크롬에서 버퍼 오버플로우 공격에 대한 취약성이 발견되었죠..
아무튼,, 이제 시작합니다.
C언어로 작성된 프로그램에서는 데이터에 지정된 버퍼의 크기보다 더 많은 양의 데이터가 입력이 되었을 시 프로그램이 비정상적으로 종료되었다. (매번 그 크기를 체크할 경우 수행 성능이 많이 떨어지기 때문이었죠.) 하지만 버퍼가 오버플로우 되는 순간에 사용자가 원하는 임의의 명령어를 수행시킬 수 있는 가능성이 알려지면서 문제가 되기 시작되었다.
우선 버퍼오버플로우 공격을 이해하려면 메모리와 스택의 구조에 대해 알아야 한다. 인텔(intel) x86계열 CPU를 사용하는 리눅스(Linux) OS를 기준으로 설명한다.

* Process memory organization
- test/data/stack 영역
* stack 영역
- LIFO (Last In First Out) 구조
- PUSH/POP operation
- procedure or function call (함수 호출 후 다음에 수행될 프로그램 주소저장)
- SP(Stack Pointer), FP(Frame Pointer)(->베이스가 될 수 있는)
- contents
paramemters, local variables, return address, previous stack frame, etc
다음의 예를 보자.
| void function(int a,int b) { char buffer1[5]; char buffer2[5]; } void main() { function(1,2); } |
 |
char 형 배열을 5byte 공간으로 잡아도 실제 메모리에서는 CPU에 따라 4 or 8 or ...이렇게 잡힌다.
두번째 예를 보자.

결과값은 0
return address를 수정했기 때문에 x=1 이 수행되지 않고 바로 printf 문이 수행되었다.
요점 - SUID 걸린 프로그램에 BOF로 공격하여 return address를 shell 띄우는 곳으로 이동하게끔 하면 root 권한을 얻을 수 있다.

C에서는 스택 크기를 원래의 크기 보다 더 크게 공간을 잡는다. 남은 빈 공간에 우리가 직접 Shell 코드를 삽입한 뒤 return address를 쉘코드가 들어가 있는 주소로 이동하게끔 해주면 되겠다.
다음글에서 직접 Shell code를 작성하여 보겠습니다.



