터너리서치에 해당되는 글 1건
2008.11.27 :: 알고리즘 코딩기법 - 부록. 최대최소는 나한테 맡겨(Ternary Search) 171
2008. 11. 27. 22:00 :: 알고리즘코딩기법
안녕하세요 조일룡입니다.
오늘은 원래 비트연산을 이용한 Brute Force Search를 하려고 했는데요..
터너리 서치는 기본적으로 위의 아이디어를 가지고 있으며 [a, b] 구간을 3등분 하여 a'과 b'을 정하고. 따라서 한번의 탐색이 이루어질 때마다 탐색구간은 2/3으로 줄어들게 됩니다.
수도코드
응용하는 의미에서 문제를 풀어봅시다.
이번 문제는 TopCoder SRM 426 Division1 에서 500점짜리로 나온 문제라 좀 어려운데요.. 터너리서치를 알고있다면 충분히 풀 수 있습니다.
"Catch The Mice" 라는 게임기가 있다. 이 게임기 안에는 장난감 쥐들이 돌아다니고 있다. 플레이어는 우리(cage)를 이동시켜 어느 순간 버튼을 눌러 cage를 떨어뜨려 cage안에 있는 쥐들을 잡을 수 있다.
쥐들은 2차원 평면상을 이동하고 이 평면은 무한히 크다고 가정해도 좋다. cage는 L*L크기의 정사각형이고 cage의 각 모서리는 축에 평행하다. 게임기의 주인은 플레이어가 cage안에 모든 쥐를 다 잡으면 스포츠카를 준다고 했지만 사실은 절대로 그런일이 발생하기를 원하지 않는다.
쥐들의 초기좌표(xp,yp)와 속도(xv,yv)가 주어졌을 때 절대로 모든쥐를 절대로 한번에 못잡게 하는 최대의 cage의 크기 L을 구하라. L의 경계에 걸린 쥐는 잡지 못한것으로 처리된다.
오늘은 원래 비트연산을 이용한 Brute Force Search를 하려고 했는데요..
갑자기 마음이 바껴서 부록으로 터너리서치를 다뤄볼까 합니다.
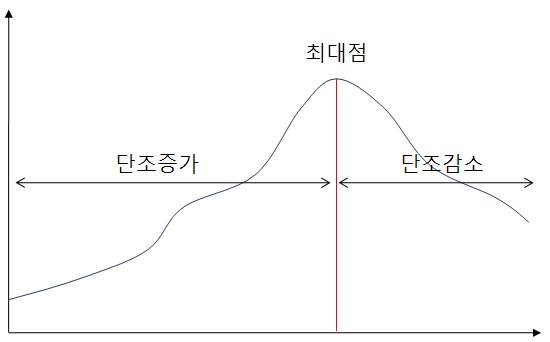
Ternary Search(터너리 서치)는 함수의 최대나 최소점을 찾는 알고리즘으로 바이너리서치와 그 동작방법이 비슷합니다.
터너리 서치로 최대점을 찾을 수 있는 함수는 최대점을 기준으로 왼쪽은 단조증가 오른쪽은 단조감소 해야합니다.
마찬가지로 최소점을 찾을 수 있는 함수는 최소점을 기준으로 왼쪽은 단조감소 오른쪽은 단조증가 해야합니다.
다시말해 지역 곡소점이나 극대점이 반드시 하나 존재해야 하고 이 점이 전역 최대나 최소점이 되어야 합니다.

최대점을 찾아보자
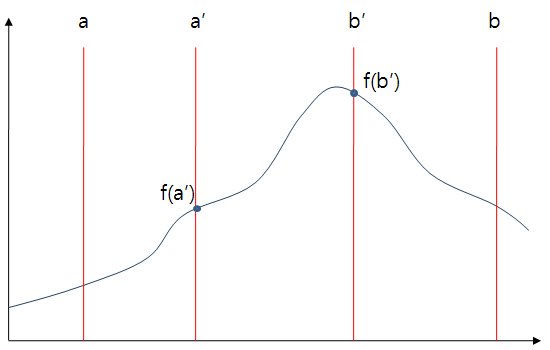
a < b 인 두 점 a, b 가 있고 함수 f(x)의 최대점이 a와 b사이에 있다고 했을 때 a < a' < b' < b 인 a'과 b'을 잡을 수 있습니다.
이때 f(a') < f(b') 이라면 [a, a'] 구간은 단조증가하고 이 구간에 f(b') 보다 더 큰 값을 가지는 점은 없습니다.
따라서 a에 a'을 대입하여 탐색구간을 좁힐 수 있습니다
반대로 f(a') > f(b') 인 경우 b에 b'을 대입하여 탑색구간을 좁힐수 있습니다.

터너리 서치는 기본적으로 위의 아이디어를 가지고 있으며 [a, b] 구간을 3등분 하여 a'과 b'을 정하고. 따라서 한번의 탐색이 이루어질 때마다 탐색구간은 2/3으로 줄어들게 됩니다.
수도코드
// [left, right] 구간내에서 함수 f(x)가 최대인 x를 구한다.
double ternarySearch(int left, int right, function& f)
{
double ternarySearch(int left, int right, function& f)
{
// 적당히 큰 수만큼 반복 -> 오차범위는 (right-left)*(2/3)^(반복횟수)
for (int i = 0; i < 1000; i++) {
double a = (left*2 + right) / 3;
double b = (left + right*2) / 3;
// 최소인 점을 찾으려면 if 문의 부호를 반대로 하면 된다.
if (f(a) < f(b))
double b = (left + right*2) / 3;
// 최소인 점을 찾으려면 if 문의 부호를 반대로 하면 된다.
if (f(a) < f(b))
left = a;
else
right = b;
}
return (left+right)/2;
return (left+right)/2;
}
응용하는 의미에서 문제를 풀어봅시다.
이번 문제는 TopCoder SRM 426 Division1 에서 500점짜리로 나온 문제라 좀 어려운데요.. 터너리서치를 알고있다면 충분히 풀 수 있습니다.
"Catch The Mice" 라는 게임기가 있다. 이 게임기 안에는 장난감 쥐들이 돌아다니고 있다. 플레이어는 우리(cage)를 이동시켜 어느 순간 버튼을 눌러 cage를 떨어뜨려 cage안에 있는 쥐들을 잡을 수 있다.
쥐들은 2차원 평면상을 이동하고 이 평면은 무한히 크다고 가정해도 좋다. cage는 L*L크기의 정사각형이고 cage의 각 모서리는 축에 평행하다. 게임기의 주인은 플레이어가 cage안에 모든 쥐를 다 잡으면 스포츠카를 준다고 했지만 사실은 절대로 그런일이 발생하기를 원하지 않는다.
쥐들의 초기좌표(xp,yp)와 속도(xv,yv)가 주어졌을 때 절대로 모든쥐를 절대로 한번에 못잡게 하는 최대의 cage의 크기 L을 구하라. L의 경계에 걸린 쥐는 잡지 못한것으로 처리된다.
풀이보기
시간 t에서 쥐의 좌표는 (xp + xv * t, yp + yv * t) 이다.
두 쥐가 있을 때 t가 변함에 따라 두 쥐를 한번에 못잡게 하는 L은 아래 그래프같은 모양이 된다.
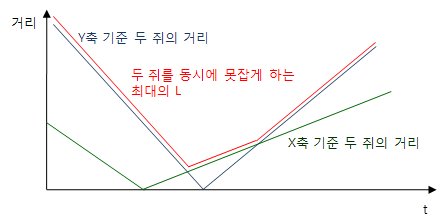
문제는 두 쥐사가 아니라 모든 쥐를 한번에 못잡게 해야 하므로 모든 쥐의 쌍에대해 그래프를 그려야 한다.
그 그래프는 아래와 같은 모양이 된다.
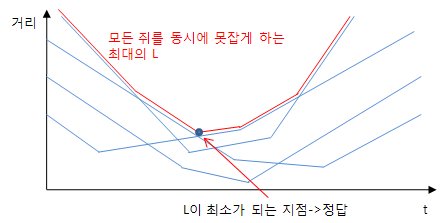
위의 그래프에서 t가 변함에 따라 모든쥐를 한번에 못잡게 하는 최대의 L도 변하게 된다. 그 중 L이 최소가 될때가 이 문제가 요구하는 정답이 된다.
문제는 저 최소점을 어떻게 구하느냐인데 L의 그래프를 살펴보면 최소점을 기준으로 왼쪽은 감소 오른쪽은 증가한다는 것을 알 수 있다. 이런 특징이 우연히 나온 것인지 아니면 모든 경우에 그런것인지를 생각해보면, 쥐들의 벡터가 어떤식으로 주어지든지 간에 모든경우에 이런 특징이 성립할것이라는 것을 예상할 수 있다.(증명은 못하겠다.;;)
그렇다면 터너리서치(Ternary Search)를 이용하여 답을 구할 수 있다.
2008/11/24 - [Study/Computer Science] - Ternary Search
두 쥐가 있을 때 t가 변함에 따라 두 쥐를 한번에 못잡게 하는 L은 아래 그래프같은 모양이 된다.

문제는 두 쥐사가 아니라 모든 쥐를 한번에 못잡게 해야 하므로 모든 쥐의 쌍에대해 그래프를 그려야 한다.
그 그래프는 아래와 같은 모양이 된다.

위의 그래프에서 t가 변함에 따라 모든쥐를 한번에 못잡게 하는 최대의 L도 변하게 된다. 그 중 L이 최소가 될때가 이 문제가 요구하는 정답이 된다.
문제는 저 최소점을 어떻게 구하느냐인데 L의 그래프를 살펴보면 최소점을 기준으로 왼쪽은 감소 오른쪽은 증가한다는 것을 알 수 있다. 이런 특징이 우연히 나온 것인지 아니면 모든 경우에 그런것인지를 생각해보면, 쥐들의 벡터가 어떤식으로 주어지든지 간에 모든경우에 이런 특징이 성립할것이라는 것을 예상할 수 있다.(증명은 못하겠다.;;)
그렇다면 터너리서치(Ternary Search)를 이용하여 답을 구할 수 있다.
2008/11/24 - [Study/Computer Science] - Ternary Search
- // 시간 t에서 모든 쥐를 한번에 잡지 못하게 하는 거리 L을 구한다.
- pair<double, pair<int, int> > func(vector <int>& xp, vector <int>& yp, vector <int>& xv, vector <int>& yv, double t)
- {
- int i, j, n = xp.size();
- double x1, y1, x2, y2;
- double maxdist = 0;
- int a,b;
- for (i = 0; i < n; i++) {
- x1 = xp[i] + xv[i]*t;
- y1 = yp[i] + yv[i]*t;
- for (j = i+1; j < n; j++) {
- x2 = xp[j] + xv[j]*t;
- y2 = yp[j] + yv[j]*t;
- double dist = MAX(abs(x1-x2), abs(y1-y2));
- if (dist > maxdist) {
- maxdist = dist;
- a = i;
- b = j;
- }
- }
- }
- return make_pair(maxdist, make_pair(a, b));
- }
- double largestCage(vector <int> xp, vector <int> yp, vector <int> xv, vector <int> yv)
- {
- int i,j,k;
- double left = 0;
- double right = 10000;
- double tl, tr, mindist;
- // 터너리서치
- for (i = 0; i < 10000; i++) {
- tl = (left*2 + right) / 3;
- tr = (left + right*2) / 3;
- pair<double, pair<int, int> > a, b, c, d;
- a = func(xp, yp, xv, yv, left);
- b = func(xp, yp, xv, yv, tl);
- c = func(xp, yp, xv, yv, tr);
- d = func(xp, yp, xv, yv, right);
- mindist = b.first;
- if (a.first == b.first) left = tl;
- else if (c.first == d.first) right = tr;
- else {
- if (b.first > c.first) left = tl;
- else right = tr;
- }
- }
- return mindist;
- }

