기말고사 시험기간인데 다들 공부 잘 하고 계신지 모르겠네요.
저는 이번 기말고사 션하게 말아먹을 것 같습니다. ㅠ
기말고사 시즌인 관계로 이번 블로그는 머리를 식힐겸 퍼즐을 하나 준비했습니다.
이건 18-2기 여러분들 들어오셨을 때 집중세미나 시간에 했던거 재탕인데요.. 뭐 뒷북이지만 괜찮겠지여 ㅋㅋ
지뢰찾기 퍼즐
지뢰찾기는 다 해보셨으리라 생각되므로 자세한 설명은 생략하겠습니다.
위의 지뢰판에서 숫자는 자기과 양옆의 칸에 있는 지뢰의 수를 알려줍니다. 한 칸에는 최대 하나의 지뢰만이 있을 수 있습니다.
그렇다면 위의 그림에는 몇 개의 지뢰가 있을까요?
지뢰찾기 고수분들은 그림 대충 보고 지뢰가 어디에 있는지 금방 찾으실거라 생각되는데여 사실 지뢰찾기 한 번도 해보지 않은 사람이라도 이 문제의 해법은 상당이 간단합니다.
답부터 말하자면 지뢰의 수는 2 + 1 + 1 + 2 = 6 입니다.
위 그림을 보면 어째서 2 + 1 + 1+ 2 가 답인지 눈치를 채실 수 있으리라 생각합니다.
붉은 색으로 표시된 칸에 적힌 숫자는 그 칸을 포함하여 양옆까지 총 3개의 칸에 존재하는 지뢰의 수를 알려줍니다. 즉 연속한 3칸을 한 단위로 보면 그 중 가운데 칸이 그 한 단위에 있는 지리의 수를 알려주는겁니다. 그렇다면 우리는 단순히 지뢰밭을 3개를 한단위로 나누어 그 각 단위별로 지뢰수를 모두 더하면 전채 지뢰밭에 있는 지뢰 수를 알게 되는 거지요.
그런데 여기에는 문제가 있습니다. 바로 이 방법은 3의 배수일때만 가능하다는 겁니다. 아래의 경우를 봅시다.
위와 같이 3개를 한단위로 쪼개보겠습니다.
그림을 보면 처음 9개의 칸에는 모두 5개의 지뢰가 있는 것을 알 수 있지만 마지막 칸에 지뢰가 있는지 없는지 확신을 가질수가 없습니다. 결국 지뢰찾기를 다 해봐야 전체 지뢰의 갯수를 알 수가 있게 됩니다. 하지만 여기에 간단한 해결책이 있습니다.
어떤가요? 전체 지뢰 갯수가 1 + 1 + 2 + 1 = 5 라는 것을 한 눈에 알 수 있습니다.
이제 우리는 아래 지뢰판에 지뢰가 몇 개인지도 쉽게 알 수 있습니다.
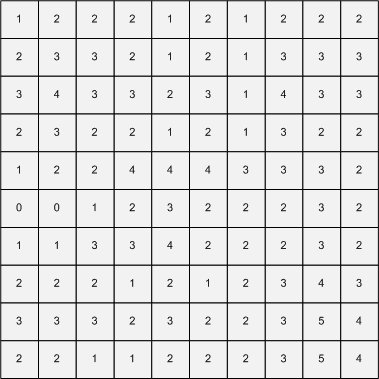
10 * 10 크기의 지뢰판인데여.. 지뢰가 어디있는지 찾으려면 힘들지만 지뢰가 몇개인지 아는 것은 이제 문제가 안됩니다.
가로세로 모두 크기가 10 (3n+1의 형태) 이므로 양쪽끝 단위의 길이는 2, 가운데는 3이 되도록 나눈뒤 가운데 칸의 수만 다 더하면 됩니다.
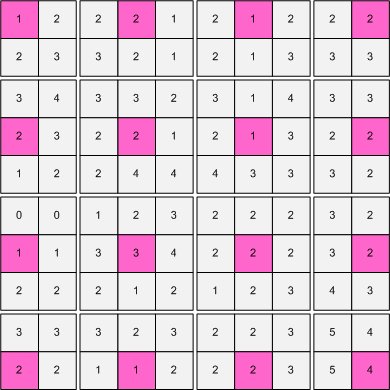
총 지뢰수는 1 + 2 + 1 + 2 + 2 + 2 + 1 + 2 + 1 + 3 + 2 + 2 + 2 + 1 + 2 + 4 = 30 이네요..
아래의 지뢰 지도를 보면 지뢰가 30개 맞다는 것을 알 수 있습니다.
(처음 지뢰판을 보고 정답표를 맞추기는 쉽지 않을것 같습니다;;)

오늘 포스팅은 여기서 마치겠습니다.
당장 보기에 어려워 보이는 문제라도 살짝 다른 시각에서 보면 간단한 해법이 존재할 수 있다는 것을 생각하시기 바랍니다.
이번에는 2진수를 이용하여 모든 경우의 수를 탐색하는 Brute Force에 대해 알아보겠습니다.
Brute Force
Brute Force는 문제를 해결할 수 있을지도 모를 모든 후보 해를 전부다 탐색하여 정말로 문제를 풀 수 있는 해를 찾는 방법입니다. 쉽게 생각해서 문제가 1 + x = 100 인 경우 이 문제의 해 x가 [0, 100] 사이의 자연수라는 것을 안다고 가정했을 때 단순히 x에 0부터 100까지 모두 대입해 보고 문제가 풀리는 x값을 찾는식의 방법입니다. 물론 저 문제를 저렇게 푸는 바보는 없어야 하겠죠?
여튼 위의 '예' 처럼 Brute Force는 해법이 간단하고 쉬운 반면 모든 후보해를 탐색해야하기 때문에 상당히 느리다라는 단점이 있습니다. 그럼에도 Brute Force를 간간히 사용하는 이유는 쉽기 때문이죠.. 그리고 모든 경우를 따지지 않고서는 도저히 해를 찾지 못하는 문제도 존재합니다.
Basic Algorithm
Brute Force를 구현하는 기본 골격을 살펴보겠습니다.
-
- first (P): generate a first candidate solution for P.
- next (P, c): generate the next candidate for P after the current one c.
- valid (P, c): check whether candidate c is a solution for P.
- output (P, c): use the solution c of P as appropriate to the application
c
 first(P)
first(P)
while c Λ do
Λ do
if valid(P,c) then output(P, c)
c next(P,c)
next(P,c)
Combinatorial explosion
안타깝게도 Brute Force는 입력크기가 커지면 사용하지 못하는 경우가 많습니다. (느리기 때문이지요)
최악의 경우
100 명의 사람들을 최적의 순으로 줄을 세우는 경우를 생각해봅시다. (어떤 경우가 최적인지는 일단 논외로 하겠습니다) 이런 문제에선 모든 경우가 몇 가지나 될까요... 100명의 사람을 순서대로 줄을 세운다.... 고등학교 때 배운 기억이... 나시나요??
기억을 더듬어보니 수학책에서 n 개의 사탕 중 r개를 순서대로 선택하는 경우의 수 nPr = n! / (n-r)! 을 본 적 있는것 같습니다.
100명의 사람중 100명을 순서대로 줄 세우는 경우의 수 = 100 P 100 = 100! / (100-100)! = 100! 이네요!!!!
경우의 수가 이처럼 팩토리얼로 나오면 입력크기가 10이 넘어가면 일반 PC로는 시간이 기하급수적으로 느려집니다. 참고로 10! = 3,628,800 입니다. 정말 참을성이 대단하더라도 입력크기가 15가 되면 15! = 1,307,674,368,000 가 되어 며칠동안 눈뜨고 기다려야 답을 볼 수 있습니다... 흠... 몇년이 될지도 모르겠네요
다른 경우를 생각해봅시다.
당신은 로또를 좋아합니다. 어디선가 잡지를 보니 로또 번호 조합에 따른 당첨 확률 계산공식이 나와 있습니다. 당신은 모든 로또 조합의 경우의 수 중 최고의 당첨 확률을 가지는 번호를 고르고 싶습니다. 한번 Brute Force로 풀어봅시다.
역시 모든 경우의 수를 따져야 하겠습니다. 로또는 45개 숫자 중 6개를 선택하죠.. 맞나요? 다시 고등학교 수학시간으로 돌아가서 n개의 사탕 중 r개를 순서에 상관없이 고르는 경우의 수는.... nCr = n! / ((n-r)! * r!) 이었군요..
45개의 숫자 중 6개를 고르는 경우의 수는 45 C 6 = (45 * 44 * 43 * 42 * 41 * 40) / (6 * 5 * 4 * 3 * 2 * 1) = 8,145,060 이네요..
뭐 이정도는 그나마 PC로 돌릴만 하겠군요....
경우의 수가 조합(Combination)으로 나오면 계산기로 간단히 계산을 해보고 이게 해뜨기전(?!)에 답을 볼 수 있는지 확인한 후 코딩을 시작해야겠습니다.
비트를 사용할 수 있고 가장 빈번히 발생하는 2^n의 경우
당신은 겁나먼 왕국의 대마법사입니다. 어느날 슈렉의 외모에 질려버린 피오나 공주가 당신에게 마법을 부려 슈렉의 외모를 바꾸고 싶어합니다. 당신은 외모를 바꾸는 n가지 마법을 가지고 있고 i번째 마법은 슈렉의 외모를 score(i)만큼 변화 시킬 것입니다. (score(i)는 음수일 수도 있습니다!!) 각 마법은 서로 독립적으로 작용하고 같은 마법을 두 번 이상 쓰더라도 점수는 한 번만 적용됩니다. 슈렉의 현재 외모 점수는 0점이고 피오나 공주는 슈렉의 외모가 정확히 S점이 되기를 원합니다. 당신은 어떤 마법을 쓰겠습니까??
이런경우 n가지의 마법을 놓고 어떤 마법을 쓰고 어떤 마법을 쓰지 않을지를 결정을 해야하겠습니다. 몇 개의 마법을 쓰는지는 자유이기 때문에 모든 경우의 수는 nC0 + nC1 + nC2 + ... + nCn = 2^n 입니다. 더 쉽게 생각하면 각각의 마법마다 쓰는 경우와 안 쓰는 경우 2가지 선택을 할 수 있는데, 마법이 n개 이므로 모두 곱하면 2^n의 경우의 수가 나옵니다.
바로 이런경우 bit연산을 이용하여 쉽게 문제를 해결할 수 있습니다.
2^20 = 약 100만 이고 2^30은 10억 입니다. PC에서 돌린다고 생각해 봤을 때 이 처럼 경우의 수가 2^n이 나오는 경우 n이 30이 넘어가면 밤샐준비를 해야 하겠습니다. (물론 밤은 PC가 새겠군요;)
Brute Force! Bit 조작해서 풀기
다른 예를 생각할 필요없이 아까전에 피오나가 낸 문제를 가지고 해보겠습니다.
당신이 부릴수 있는 마법이 20개라고 합시다. 그리고 각각의 마법에 따른 용모의 변화가 벡터 score로 넘어옵니다. 마법의 점수 합이 S가 되는 모든 경우에 대해 사용하는 마법의 번호(0~19)를 오름차순으로 출력하는 함수를 작성하겠습니다.
- //////////////////////////////////////////////////////////////////////
- //
- // void Magic(vector<int> socre, int S)
- // 슈렉의 외모를 S로 만드는 마법의 조합을 찾는다
- //
- // vector<int> score : i번째 마법이 슈렉의 외모점수를 socre[i]만큼 변화시킨다
- // int S : 피오나가 원하는 슈렉의 외모 점수
- //
- void Magic(vector<int> score, int S)
- {
- int i = 0, j = 0;
- int n = score.size(); // 마법의 갯수
- // 모든 경우(2^n)를 탐색
- for (i = 0; i < (1 << n); i++)
- {
- // 사용하는 마법의 점수 합
- int sum = 0;
- // 모든 마법 탐색
- for (j = 0; j < n; j++)
- {
- // i의 경우 j번째 마법을 사용 하는가?
- if (i & (1 << j))
- {
- // j번째 사용한다면 점수는 score[j]만큼 변한다.
- sum += score[j];
- }
- }
- // 사용한 마법의 점수 합이 S이면 마법 출력
- if (sum == S)
- {
- // 모든 마법 탐색
- for (j = 0; j < n; j++)
- {
- // j번째 마법을 사용했으면 출력
- if (i & (1 << j))
- {
- cout << j << " ";
- }
- }
- cout << endl;
- }
- }
- }
같은 문제를 DFS로 구현하는 백트레킹(backtracking)으로도 풀 수 있습니다.
- //////////////////////////////////////////////////////////////////////
- //
- // void MagicBacktrack(vector<int>& score, int S, int index, int use)
- // 슈렉의 외모를 S로 만드는 마법의 조합을 찾는다(백트레킹)
- //
- // vector<int>& score : i번째 마법이 슈렉의 외모점수를 socre[i]만큼 변화시킨다
- // int S : 피오나가 원하는 슈렉의 외모 점수
- // int index : index 번째의 마법을 사용할지 안할지를 검사함
- // int use : use의 i번째 bit가 1이면 i번째 마법을 사용하기로 결정함
- // int sum : 사용하기로 한 마법의 점수 합
- //
- void MagicBacktrack(vector<int>& score, int S, int index, int use, int sum)
- {
- // 마법의 수
- int n = score.size();
- // 모든 마법에 대해 선택 여부를 결정했음
- if (index == n)
- {
- // 선택한 마법의 합이 S -> 선택한 마법을 출력
- if (sum == S)
- {
- // n개의 마법을 탐샙
- for (int i = 0; i < n; i++)
- {
- // i번째 마법을 사용하기로 했네요
- if (use & (1 << i))
- {
- cout << i << " ";
- }
- }
- cout << endl;
- }
- return;
- }
- /* 마법점수가 양수만 존재한다면 아래 가지치기로 탐색범위를 줄일 수 있다.
- if (sum > S)
- {
- return;
- }
- */
- // index 번째 마법을 사용하기로 결정함
- MagicBacktrack(score, S, index + 1, use | (1 << index), sum + score[index]);
- // index 번째 마법을 사용 안하기로 결정함
- MagicBacktrack(score, S, index + 1, use, sum);
- }
- int main()
- {
- // 함수가 잘 도나 테스트 해보는 코드입니다.
- vector<int> score;
- score.push_back(15);
- score.push_back(13);
- score.push_back(-5);
- score.push_back(7);
- score.push_back(55);
- score.push_back(12);
- score.push_back(3);
- score.push_back(1);
- score.push_back(-11);
- score.push_back(-6);
- score.push_back(4);
- MagicBacktrack(score, 47, 0, 0, 0);
- }
DFS의 기본은 알고리즘 코딩기법 - 3. 재귀호출을 참고하시면 됩니다. 백트레킹에 대해서는 혹시나 마음이 내키면 포스팅 하겠습니다.
오늘은 원래 비트연산을 이용한 Brute Force Search를 하려고 했는데요..
갑자기 마음이 바껴서 부록으로 터너리서치를 다뤄볼까 합니다.
Ternary Search(터너리 서치)는 함수의 최대나 최소점을 찾는 알고리즘으로 바이너리서치와 그 동작방법이 비슷합니다.
터너리 서치로 최대점을 찾을 수 있는 함수는 최대점을 기준으로 왼쪽은 단조증가 오른쪽은 단조감소 해야합니다.
마찬가지로 최소점을 찾을 수 있는 함수는 최소점을 기준으로 왼쪽은 단조감소 오른쪽은 단조증가 해야합니다.
다시말해 지역 곡소점이나 극대점이 반드시 하나 존재해야 하고 이 점이 전역 최대나 최소점이 되어야 합니다.
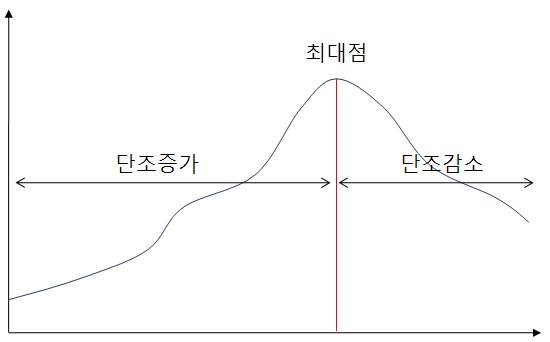
최대점을 찾아보자
a < b 인 두 점 a, b 가 있고 함수 f(x)의 최대점이 a와 b사이에 있다고 했을 때 a < a' < b' < b 인 a'과 b'을 잡을 수 있습니다.
이때 f(a') < f(b') 이라면 [a, a'] 구간은 단조증가하고 이 구간에 f(b') 보다 더 큰 값을 가지는 점은 없습니다.
따라서 a에 a'을 대입하여 탐색구간을 좁힐 수 있습니다
반대로 f(a') > f(b') 인 경우 b에 b'을 대입하여 탑색구간을 좁힐수 있습니다.
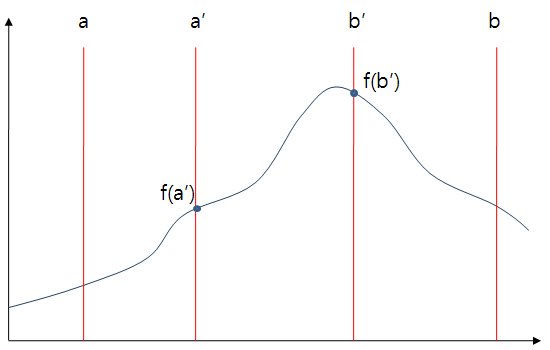
터너리 서치는 기본적으로 위의 아이디어를 가지고 있으며 [a, b] 구간을 3등분 하여 a'과 b'을 정하고. 따라서 한번의 탐색이 이루어질 때마다 탐색구간은 2/3으로 줄어들게 됩니다.
수도코드
double ternarySearch(int left, int right, function& f)
{
double b = (left + right*2) / 3;
// 최소인 점을 찾으려면 if 문의 부호를 반대로 하면 된다.
if (f(a) < f(b))
return (left+right)/2;
응용하는 의미에서 문제를 풀어봅시다.
이번 문제는 TopCoder SRM 426 Division1 에서 500점짜리로 나온 문제라 좀 어려운데요.. 터너리서치를 알고있다면 충분히 풀 수 있습니다.
"Catch The Mice" 라는 게임기가 있다. 이 게임기 안에는 장난감 쥐들이 돌아다니고 있다. 플레이어는 우리(cage)를 이동시켜 어느 순간 버튼을 눌러 cage를 떨어뜨려 cage안에 있는 쥐들을 잡을 수 있다.
쥐들은 2차원 평면상을 이동하고 이 평면은 무한히 크다고 가정해도 좋다. cage는 L*L크기의 정사각형이고 cage의 각 모서리는 축에 평행하다. 게임기의 주인은 플레이어가 cage안에 모든 쥐를 다 잡으면 스포츠카를 준다고 했지만 사실은 절대로 그런일이 발생하기를 원하지 않는다.
쥐들의 초기좌표(xp,yp)와 속도(xv,yv)가 주어졌을 때 절대로 모든쥐를 절대로 한번에 못잡게 하는 최대의 cage의 크기 L을 구하라. L의 경계에 걸린 쥐는 잡지 못한것으로 처리된다.
풀이보기
두 쥐가 있을 때 t가 변함에 따라 두 쥐를 한번에 못잡게 하는 L은 아래 그래프같은 모양이 된다.
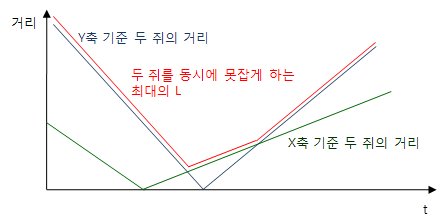
문제는 두 쥐사가 아니라 모든 쥐를 한번에 못잡게 해야 하므로 모든 쥐의 쌍에대해 그래프를 그려야 한다.
그 그래프는 아래와 같은 모양이 된다.
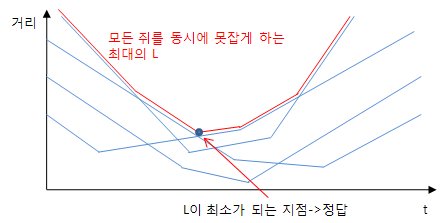
위의 그래프에서 t가 변함에 따라 모든쥐를 한번에 못잡게 하는 최대의 L도 변하게 된다. 그 중 L이 최소가 될때가 이 문제가 요구하는 정답이 된다.
문제는 저 최소점을 어떻게 구하느냐인데 L의 그래프를 살펴보면 최소점을 기준으로 왼쪽은 감소 오른쪽은 증가한다는 것을 알 수 있다. 이런 특징이 우연히 나온 것인지 아니면 모든 경우에 그런것인지를 생각해보면, 쥐들의 벡터가 어떤식으로 주어지든지 간에 모든경우에 이런 특징이 성립할것이라는 것을 예상할 수 있다.(증명은 못하겠다.;;)
그렇다면 터너리서치(Ternary Search)를 이용하여 답을 구할 수 있다.
2008/11/24 - [Study/Computer Science] - Ternary Search
- // 시간 t에서 모든 쥐를 한번에 잡지 못하게 하는 거리 L을 구한다.
- pair<double, pair<int, int> > func(vector <int>& xp, vector <int>& yp, vector <int>& xv, vector <int>& yv, double t)
- {
- int i, j, n = xp.size();
- double x1, y1, x2, y2;
- double maxdist = 0;
- int a,b;
- for (i = 0; i < n; i++) {
- x1 = xp[i] + xv[i]*t;
- y1 = yp[i] + yv[i]*t;
- for (j = i+1; j < n; j++) {
- x2 = xp[j] + xv[j]*t;
- y2 = yp[j] + yv[j]*t;
- double dist = MAX(abs(x1-x2), abs(y1-y2));
- if (dist > maxdist) {
- maxdist = dist;
- a = i;
- b = j;
- }
- }
- }
- return make_pair(maxdist, make_pair(a, b));
- }
- double largestCage(vector <int> xp, vector <int> yp, vector <int> xv, vector <int> yv)
- {
- int i,j,k;
- double left = 0;
- double right = 10000;
- double tl, tr, mindist;
- // 터너리서치
- for (i = 0; i < 10000; i++) {
- tl = (left*2 + right) / 3;
- tr = (left + right*2) / 3;
- pair<double, pair<int, int> > a, b, c, d;
- a = func(xp, yp, xv, yv, left);
- b = func(xp, yp, xv, yv, tl);
- c = func(xp, yp, xv, yv, tr);
- d = func(xp, yp, xv, yv, right);
- mindist = b.first;
- if (a.first == b.first) left = tl;
- else if (c.first == d.first) right = tr;
- else {
- if (b.first > c.first) left = tl;
- else right = tr;
- }
- }
- return mindist;
- }
많은 경우에 어떤 상태는 Yes나 No로 나타낼 수 있습니다.
예를 들면 쟁반위에 사과가 있냐/없냐 와 같은 상태가 있을 수 이겠네요. 초기에 쟁반위에 사과, 배, 참외, 수박, 포도가 있었는데 누군가 과일을 먹어서 어떤 것은 없어졌습니다. 이때 가능한 상태는 모두 32(=2^5)가지가 됩니다.
프로그램을 작성하면서 위와 같은 상태를 나타내야 하는 경우는 종종 발생합니다. 그리고 어떻게든 나타내게 되겠지요..
각각의 과일마다 boolean type의 변수를 하나식 만들 수도 있고 좀 더 똑똑한 누군가는 boolean type의 배열을 선언할 수도 있습니다.
오늘 포스팅에서는 bit를 이용하여 이런 상황을 표현하는 방법을 알아보겠습니다.
bitwise AND는 두 바이너리 표현에 대해서 각 비트의 쌍마다 AND 연산을 합니다.
AND 0011
= 0001
C++ 에서 bitwise AND 연산자는 &입니다. 반면 logical AND 연산자는 &&입니다. 사용할 때 주의를 해야겠지요.
bitwise AND 연산은 주로 bitmask를 취할때 사용합니다. 가령 어떤 바이너리에 대해서 첫번째 비트와 세번째 비트를 취하고 싶다면 bitwise AND 0101(2) 를 취하면 됩니다.
bitwise OR
bitwise OR은 두 바이너리 표현에 대해서 각 비트의 쌍마다 OR 연산을 합니다.
OR 0011
= 0111
C++에서 bitwise OR 연산자는 |입니다. 마찬가지로 logical OR연산자인 ||와 혼돈할 가능성이 크니 주의해야겠습니다.
bitwise OR 연산은 바이너리 표현에 플레그(flag)를 추가할때 사용합니다. 각 비트마다 어떤 의미를 부여한 사항에서 첫번째 비트와 세번째 비트에 해당하는 의미가 추가되었다면 원래 상태에다가 새로 추가된 상태를 더해야 합니다. 이때 bitwise OR을 사용합니다.
bitwise XOR
bitwise XOR은 두 바이너리 표현에 대해서 각 비트의 쌍마다 XOR 연산을 합니다.
XOR 0011
= 0110
C++에서 bitwise XOR 연산자는 ^입니다. AND나 OR과 다르게 logical XOR 연산자는 c++에 없습니다.
위의 예에서와 같이 bitwise XOR 연산은 바이너리 표현에에서 특정 비트를 토글(toggle)할때 사용합니다. 비트열 중 어떤 상태를 나타내는 비트를 반전시켜줘야 할때 반전 시켜야할 비트만 1로 세팅해놓고 bitwise XOR를 취하면 됩니다.
bitwise NOT(complement)
bitwise XOR은 두 바이너리 표현에 대해서 각 비트의 쌍마다 NOT 연산을 합니다.
= 1010
C++에서 bitwise NOT 연산자는 ~입니다. logical NOT 연산자는 !이니 햇갈릴일은 거의 없겠네요
bitwise NOT은 모든 비트를 반전합니다.
참고
http://en.wikipedia.org/wiki/Bit_operation
사과, 배, 참외, 수박, 포도
이제 비트열을 이용하여 과일의 상태를 나타내보도록 하겠습니다. 그리고 배열을 사용한 방법과 비교를 해보도록 하겠습니다
비트에 의미부여
과일의 종류가 5가지 이므로 다섯비트가 필요합니다.
첫번째 비트부터 다섯번째 비트까지 각각 사과, 배, 참외, 수박, 포도가 있는지 없는지 여부를 나타내는 상태라고 생각합시다. 과일이 있으면 그 비트는 1이 되고 비트가 0이면 그 과일이 없다는 것을 의미합니다.
5개의 비트를 저장할 변수가 필요한데 현재 C++에서 int는 32bit 정수형이므로 5개의 과일의 상태를 저장하고도(5bit사용) 27bit나 남으므로 int형을 사용하겠습니다.
초기상태
처음에는 과일이 모두 있으므로 아래와 같이 초기 상태를 설정할 수 있습니다.
int bitFruits[] = {(1<<0), (1<<1), (1<<2), (1<<3), (1<<4)}; // 사과, 배, 참외, 수박, 포도를 나타내는 비트
int fruits = (1<<numFruits) - 1; // 모든 과일이 있다
(1 << 5) - 1에 대해 간략히 살펴봅시다.
1을 이진수로 나타내면 00000001(2)입니다. << 5 연산은 이 바이너리를 왼쪽(더 큰 비트쪽)으로 5번 이동합니다. 그럼 00100000(2)가 됩니다. 여기에서 1을 빼면 00011111(2)가 됩니다. 어떤가요? 다섯개의 과일이 모두 있다는 상태가 되었네요
배열버전
bool fruits[numFruits] = {true, true, true, true, true}; // 모든 과일이 있다.
누군가 과일을 먹는다
A가 지나가다 쟁반에 과일이 놓여져 있는 것을 보고 자기가 젤 좋아하는 수박을 먹었습니다. 이를 아래와 같이 코드로 옮길 수 있습니다.
fruits &= ~eatA; // A가 과일을 먹음 - 수박을 먹어서 없어짐
bitwise NOT, bitwise AND 연산을 이용하여 수박에 해당하는 비트를 0으로 변환하였습니다.
연산 후 frutis은 10111(2)가 됩니다.
배열버전
// B가 과일을 먹음
for (int i = 0; i < numFruits; i++)
if (eatA[i] == true)
fruits[i] = false;
이번엔 B가 지나가다 쟁반을 보았습니다. B는 욕심이 많아서 배, 수박, 포도를 먹으려 합니다. 아래 코드를 봅시다.
int eatByB = fruits & eatB; // B가 실제로 먹는 과일
fruits &= ~eatB; // B가 과일을 먹음
bitwise OR 연산을 이용하여 B가 먹고싶은 과일들의 비트를 만듭니다. 그 후 먹는 것은 A때와 같습니다.
여기에서 수박은 A가 이미 먹었기 때문에 B가 먹을 수는 없습니다. B가 먹을 수 있는 과일은 자기가 먹으려고 하면서 쟁반에 놓여져 있어야 합니다. eatByB는 B가 실제로 먹게되는 과일을 bitwise AND 연산으로 구합니다.
연산후 eatByB와 fruits는 다음과 같습니다.
eatByB = 10111(2) & 11010(2) = 10010(2) -> 배, 포도
fruits = 10111(2) & (~11010(2)) = 10111(2) & 00101(2) = 00101(2) -> 사과, 참외
배열버전
int eatByB[numFruits] = {false};
for (int i = 0; i < numFruits; i++)
{
// B가 실제로 먹는 과일
if (fruits[i] && eat[i])
eatByB[i] = true;
// B가 과일을 먹음
if (eat[i] == true)
fruits[i] = false;
}
어떤 과일이 없어진거지??
A랑 B가 과일을 먹어서 몇개의 과일이 없어진 것을 나중에 알게된 쟁반의 주인은 어떤 과일이 없어졌는지 알고 싶습니다.
쟁반의 주인은 bitwise NOT연산으로 어떤 과일이 없어졌는지 금새 알아차립니다.
배열버전
for (int i = 0; i < numFruits; i++)
if (fruits[i] == false)
disappeared[i] = true;
사과 마니아 등장
사과를 엄청나게 좋아하는 A씨가 있습니다. A씨는 사과를 너무 좋아해서 쟁반에 사과가 있으면 그 사과를 먹을 것입니다. 반면 쟁반에 사과가 없으면 자기가 가지고 있던 사과를 쟁반에 올려놓는다고 합니다. A씨가 쟁반을 본다면 어떤일이 일어날까요?
fruits &= ~bitFruits[0]; // 사과를 먹는다
else // 사과가 없으면
fruits |= bitFruits[0]; // 사과를 쟁반에 놓는다
배열버전
fruits[0] = false; // 사과를 먹는다
else // 사과가 없으면
fruits[0] = true; // 사과를 쟁반에 놓는다.
Bitwiase 표기 vs 배열표기
yes/no로 나타낼 수 있는 일련의 상태가 있을 때, 이 상태를 나타낼 수 있는 두 가지 방법(비트, 배열)에 대해서 간략히 살펴보았는데요.. 구현의 예에서 드러나듯이 bit를 사용하는 방법이 속도, 메모리, 구현 측면에서 모두 배열을 사용하는 방법보다 월등히 뛰어납니다. (물론 제 생각이긴 합니다) 한가지 단점이 있다면 나타내야할 상태의 공간이 크다면(예를 들어 50개 정도되는 상태는 int변수에 담을 수 없으니깐여;;) bit를 사용하기 힘들어 지는데 이때는 다른 방법을 강구해 봐야겠지요.. 배열을 쓰는것도 방법이 될 수 있습니다.
다행이도 long long(__int64) 이라는 타입은 64bit를 지원합니다. 이 타입을 이용하면 64개의 독립된 변수를 가진 상태까진 하나의 변수를 이용하여 나타낼 수 있습니다.
이번 포스팅에서 bit를 이용한 상태표현에 대해서 알아보았으니 다음 포스팅에서는 bit를 이용한 brute force방법에 대해 알아보겠습니다.
ps.
제가 포스팅하는 소스에는 무한버그가 있을 수도 있습니다. -ㅁ-;;
안녕하세요 조일룡입니다.
오늘은 C++에서 표준 라이브러리로 채택된 STL에 대해 간략하게 알아보겠습니다.
STL은 Standard Template Library의 약자로 템플릿을 이용한 표준 라이브러리.. 뭐 이정도의 의미를 가지고 있습니다.
아래의 주소에서 STL에 대한 모든것을 알 수 있습니다.
http://www.cplusplus.com/reference/stl/
이번 포스팅에서는 템플릿에대해 잠깐 짚어보고, STL에서 제공하는 컨테이너 중 가장 흔히 사용하는 'vector'에 대해 알아보겠습니다.
Template
템플릿을 건너뛰고 싶었지만 역시 언급을 해야할 것 같습니다.
템플릿은 컴파일타임에 자료형을 확정하여 그 자료형에 맞는 코드를 생성하는 C++에서 제공하는 기능입니다.
두개의 정수형 변수를 받아 값을 맞바꾸는 아래의 함수를 봅시다.
{
만약 실수형 변수를 받아 똑같은 일을 하는 함수가 필요하다면 우리는 아래와 같은 함수를 재정의 해야합니다.
{
단지 자료형만 다를 뿐 함수의 몸체는 동일한 구조를 가진 함수를 따로 구현하려니 여간 귀찮은 일이 아닙니다. 그래도 함수를 구현하는 일이니 좀 참아줄만 하네요.. 근데 클레스에서 이 짓을 해야한다면 참을 수 있을까요?
한 프로그램에서 int 형의 자료를 저장하는 스택과 double 형의 자료를 저장하는 스택이 필요한 경우를 가정해봅시다. 이 때 두 가지 형태의 스택을 각각 구현하려 생각하는 짜증이 밀려 오는군요... 하지만 어쩔수 없이 노가다 근성으로 코딩을 하겠지요.
일단 int형 스택을 구현하고 control+C -> contro+V 콤보를 작렬한 후 replace all(int->double)을 감행합니다.
휴.. 그나마 붙여넣기, 모두바꾸기 신공으로 그렇게 큰 노력을 들이지 않고 각각의 클레스를 만들긴 했습니다. ^^;
그런데 프로그램을 실행하다 보니 이상하게 프로그램이 죽는군요.. 어디가 잘못됐는지 찾아보니 스택이 문제입니다..
열심히 디버깅을 해서 오류가 난 지점을 찾아 제대로 작동하게 고쳤습니다.
이제 다시 프로그램을 실행하는데.. 또 죽는군요.. 이건 또 뭘까요.. 디버그를 해서 찾아보니...
아.. 아까전에 int형 스택만 고치고 double형 스택은 안고쳤네요 ㅠㅠ
템플릿을 사용하여 swap을 구현해봅시다.
void swap(ItemType & a, ItemType & b)
{
a = b;
b = temp;
위의 swap과 모양이 약간 다른데요.. 위의 swap에서는 비트연산을 통해 두 변수의 값을 맞바꾸었지만 아래에서는 temp변수를 사용해서 바꿨습니다.
template을 통해 넘어오는 변수의 자료형이 비트연산으로 값을 맞바꿀수 없는 경우가 있을 수 있기 때문인데요.. 예를 들어 string같은 자료형은 비트연산으로 그 값을 맞바꿀 수 없지요.. 대신 저렇게 해야합니다. 물론 대입연산자 재정의는 필수입니다.
Template의 원리
제 경험상 많은 친구들이 template의 사용은 잘 하지만 이게 어떻게 동작하는지는 잘 모릅니다. 어떤 친구는 런타임시에 어떤 메커니즘이 작동하는거 아니냐고 하더군요 그렇기 때문에 template을 쓰면 속도가 느려진다고 하면서...
그 친구에게 유감스럽지만 template은 런타임시에 자료형을 보고 적절한 처리를 하는 것이 아닙니다. C++ 컴파일러가 그렇게까지 똑똑하진 않나봅니다. 사실은 그렇게까지 똑똑해질 필요는 없습니다.
C++은 단지 컴파일시간에 template으로 작성된 함수나 클래스를 사용하는 클라이언트를 보고 필요한 자료형으로 확장된 함수나 클레스를 각각 만들어 줍니다. 그러니깐 붙여넣기 + 모두바꾸기 신공을 컴파일러가 해주는 샘이지요 ㅎㅎ.. 컴파일이 약간 느려질수는 있겠습니다만 템플릿 때문에 실행속도가 느려졌다는 말은 어불성설이겠네요..
vector
vector는 STL에서 제공하는 컨테이너중 하나로 제 생각엔 가장많이 사용되는 컨테이너가 아닐까 생각됩니다.
vector는 배열과 같은 일을 합니다. 연속적인 공간에 템플릿으로 정의된 자료형의 배열을 할당하여 그 후에는 배열처럼 사용할 수 있습니다. 그리고 여러 STL에서 제공되는 algorithm 함수와 함께 강력한 기능을 제공합니다.
vector vs array
c++에선 이미 배열을 기본 데이터타입으로 제공을 합니다. 그런데 vector를 쓰는 이유는 무엇일까요?
가장 큰 이유는 동적할당 때문일 겁니다.
c++에서 배열을 잡을 때 컴파일시간에 배열의 크기를 모르면 배열을 잡을 수 없습니다. 즉 배열의 크기는 변수가 될 수 없고 오로지 상수만이 가능합니다. 이를 극복하기 위해 동적할당이 제공됩니다. c에서는 malloc 함수를 쓰고 c++에서는 new 객체를 사용합니다.
위의 기능을 활용하여 런타임에 적절한 배열의 크기를 알아내서 적절하게 배열을 할당할 수 있습니다.
그럼 왜 vector일까요?
런타임시에도 배열을 얼마나 크게 잡아야 할지 모르는 경우를 생각해봅시다. 예를 들어 장기게임을 하는데 한 수 한 수를 배열에 저장하고 싶습니다. 그런데 장기게임이 몇 수 만에 끝날지는 아무도 모르기 때문에 배열을 잡기가 쉽지 않습니다.
방법중 하나로 배열을 그냥 대충 엄하게 크게 할당하고 시작할 수는 있습니다. 왠만하면 그 배열크기를 초과할 만큼 게임이 진행되지는 않게 크게 잡습니다. 대부분의 게임은 배열을 오버플로우를 발생시키지 않고 종료됩니다. 하지만 여기에는 두가지의 문제점이 있습니다.
첫번재 문제점은 메모리의 낭비입니다. 대부분의 경우 잡아놓은 배열을 다 쓰지 않고 버려진채 게임이 끝납니다.
두번째 문제점은 메모리 오버플로우의 가능성이 있다는 것입니다. 두 기사가 너무 방어적이라 좀처럼 게임이 끝나지 않고 계속 진행되다 보면 잡아놓은 배열을 모두 쓰고도 모자란 상황이 발생할 수 있습니다. 이때 게임은 외마디 오류박스를 띄우고 사라지겠지요.
위의 문제를 해결하기 위해서 일단 배열을 적당히 작게 잡고 필요할때마다 더 큰 배열을 할당하는 방법이 있습니다. 장기를 예로 보면 대부분 장기를 하면 50수까지는 둔다는 정보가 있다고 가정합시다. 그럼 첫 번째 배열은 크기를 50으로 잡습니다. 게임이 진행되다가 50수가 넘으면 100개짜리 배열을 새로 잡고 50수까지의 기록을 100개 짜리 배열에 복사를 합니다. 그후 50개짜리 배열은 메모리에서 해제를 하고 이제부턴 100개짜리 배열을 씁니다. 이런식으로 배열의 크기가 더 커질 필요가 있을 때 마다 새로 메모리를 할당하는 방법이 있습니다만. 귀차니즘이 텍사스 소때처럼 몰려옵니다.
만약 한 프로그램내에서 저런 배열이 여러개 있어야 한다면 각각 구현해야 하는데 정말 귀찮아 죽겠습니다. 그렇다면 객체지향프로그래밍 페러다임을 도입해 클래스로 저런 배열을 구현해 놓고 가져다 쓰는게 그나마 좀 영리한 선택이 되겠지요? 거기에다가 템플릿의 편리함 까지 추가해서 언제어디서나 쓸 수 있게 만들어 놓읍시다.. ㅋㅋㅋ 클래스를 구현할땐 좀 귀찮지만 나중을 생각하면 기분좋은 일이내요
그런데 C++을 사용하는 프로그래머들에게 사막 한 가운데의 오아시스 같은 존재가 있었으니 그것이 바로 STL입니다.
STL에선 바로 저런 배열 클레스를 vector라는 이름으로 제공을 하고 있습니다. 저 같은 귀차니즘에 감염된 종자들에게 구원의 손길과 같게 느껴지네요.
vector를 사용해보자
우선 vector의 멤버함수를 살펴봅시다.
Member functions
| (constructor) | Construct vector (public member function) |
| (destructor) | Vector destructor (public member function) |
| operator= | Copy vector content (public member function) |
Iterators:
| begin | Return iterator to beginning (public member type) |
| end | Return iterator to end (public member function) |
| rbegin | Return reverse iterator to reverse beginning (public member function) |
| rend | Return reverse iterator to reverse end (public member function) |
Capacity:
| size | Return size (public member function) |
| max_size | Return maximum size (public member function) |
| resize | Change size (public member function) |
| capacity | Return size of allocated storage capacity (public member function) |
| empty | Test whether vector is empty (public member function) |
| reserve | Request a change in capacity (public member function) |
Element access:
| operator[] | Access element (public member function) |
| at | Access element (public member function) |
| front | Access first element (public member function) |
| back | Access last element (public member function) |
Modifiers:
| assign | Assign vector content (public member function) |
| push_back | Add element at the end (public member function) |
| pop_back | Delete last element (public member function) |
| insert | Insert elements (public member function) |
| erase | Erase elements (public member function) |
| swap | Swap content (public member function) |
| clear | Clear content (public member function) |
Allocator:
| get_allocator | Get allocator (public member function) |
http://www.cplusplus.com/reference/stl/vector/
100개의 숫자를 임의로 생성하고 비내림차순으로 소팅하여 출력하는 아래의 프로그램을 봅시다.
- #include <cstdlib>
- #include <ctime>
- #include <iostream>
- #include <vector>
- #include <algorithm>
- using namespace std;
- int main()
- {
- int i;
- srand(time(NULL));
- // 벡터를 선언합니다
- vector<int> nums;
- // 100개의 난수를 생성하여 벡터에 추가합니다
- for (i = 0; i < 100; i++)
- nums.push_back(rand());
- // 비내림차순으로 정렬
- sort(nums.begin(), nums.end());
- // 화면에 출력
- for (i = 0; i < 100; i++)
- cout << nums[i] << endl;
- return 0;
- }
위의 프로그램에서는 push_back() 함수를 사용하였습니다만 vector에 추가될 원소의 갯수를 미리 알고 있다면 생성자에서 미리 배열의 크기를 지정하여 시간과 메모리를 아낄 수 있습니다.
- int main()
- {
- int i;
- srand(time(NULL));
- int N = 100;
- vector<int> nums(N, 0);
- for (i = 0; i < N; i++)
- nums[i] = rand();
- sort(nums.begin(), nums.end());
- for (i = 0; i < N; i++)
- cout << nums[i] << endl;
- return 0;
- }
마지막으로 vector<int> 형 배열을 전달받아 합과 평균을 리턴하는 함수를 작성해보겠습니다. 평균은 반올림합니다.
- vector<int> SumAvg(vector<int> array)
- {
- vector<int> ans;
- int sum = 0;
- for (int i = 0; i < array.size(); i++)
- {
- sum += array[i];
- }
- ans.push_back(sum);
- ans.push_back((double)ans / array.size() + 0.5);
- return ans;
- }
이것으로 이번 포스팅은 마치겠습니다. 힘드네요 ^^;
다음 포스팅은 비트연산(bit operation)을 이용한 Brute Force Search 방법에 대해서 쓸까합니다. 간략히 설명하자면 Brute Force는 해의 후보가 될 수 있는 모든 문제 공간을 탑색하여 최적을 찾는 방법입니다. 문제를 해결하는 가장 확실하면서도 쉬운 방법인 반면에 수행 시간이 긴 단점이 있죠.. 주로 모든 문제 공간을 탐색해야 하는 경우에 사용됩니다.
안녕하세요.
오늘은 바이너리서치(Binary Search) 의 코딩법에 대해서 알아보겠습니다.
숫자맞추기
참이슬을 까고나면 병뚜껑을 꼬은 다음에 손가락으로 쳐서 끊어지면 그 전사람이 벌주를 마시는 게임이 있죠?? 그리고 나서 벌주를 마신 사람은 병뚜껑에 있는 숫자를 보고 업&다운을 해서 그 숫자를 부른 사람이 또 벌주를 마십니다. (이거 우리 학교만 하나요?)
혹시나 모르시는 분이 있을까봐 부가 설명을 드리겠습니다.
참이슬 병뚜껑에는 [1, 50] 사이의 숫자가 찍혀있습니다. 한사람씩 숫자를 부르면 정답을 아는 사람이 정답에 지금 부른 숫자보다 큰지 작은지를 알려줍니다. 그 다음 사람은 좁혀진 범위 내에서 숫자를 다시 부릅니다. 그럼 범위가 점점 좁혀지고 누군가 숫자를 맞추게 되는데 그 사람이 벌주를 마시게 됩니다.
이 게임을 하고 있는 모든 사람이 화장실을 가고 싶어서 최대한 게임을 빨리 끝내기위해 최선을 다한다면 최대 몇 번째 사람까지 턴이 돌아갈까요??
그렇습니다. 정답은 6회입니다. 확인을 위해 검증을 해보도록 하겠습니다.
2회: [26, 50] - 38을 부름 [26, 37], [39, 50] 모두 12개의 숫자가 남아있으므로 어떤 범위가 남아도 최소횟수는 같음
3회: [26, 37] - 31을 부름 [26, 30], [32, 37] 중 [32, 37]이 숫자가 하나 더 많으므로 최악의 경우는 [32, 37]
4회: [32, 37] - 35를 부름 [32, 34], [36, 37] 중 [32, 34]가 숫자가 하나 더 많으므로 최악의 경우는 [32, 34]
5회: [32, 34] - 33을 부름 [32, 32], [34, 34] 모두 하나만 남았음
6회: 하나만 남았습니다. 번호를 부르고 소주를 원샷하세요
모든 사람이 최선을 다 했을때 숫자가 하나가 남을때까지 게임이 지속된 예를 들었는데요. 이를 수식화 하여 풀 수 있습니다.
한 턴이 지날때 마다 숫자의 범위가 반씩 줄어들게 됩니다. n번째 턴에서 남은 숫자의 범위를 T(n)이라 하면,
T(n) = ceiling[ 0.5 * T(n-1) ] , ceiling은 올림입니다.
이 되고 식을 마스터정리(Master theorem)을 이용하여 풀면
T(n) = O(lg n) 이 됩니다. (여기서 lg는 밑이 2인 로그입니다)
아까 소주게임에 적용해 보면 n이 50 이므로 ceiling[ lg 50 ] = 6 이 되는것을 확인할 수 있습니다.
이처럼 바이너리서치를 적용하면 한 턴이 지날때마나 남아있는 후보의 범위를 반으로 팍팍 줄여나가기 때문에 검색을 해야하는 경우 아주 강력한 도구가 될 수 있습니다.
생각보다 어려운 바이너리서치
Knuth는 <Sorting and Searching>에서 이진탐색이 처음 발표된 것은 1946년이고, 버그가 없는 최초의 이진탐색 코드는 1962년이 되어서야 나타났다고 지적했습니다. 버그프리한 바이너리서치루틴도 보면 정말 간단합니다. 왜 이렇게 간단한걸 작성하는데 20년이나 걸렸는지 생각해 보면 그 만큼 버그없는 프로그램을 만든다는 것이 어려운 일이고 tricky한 버그를 발견하기도 쉬운일이 아닌가 봅니다.
아래의 의사코드를 봅시다.
INT U = N // 상한
INT Solution = -1 // 원하는 결과가 있는 위치 (-1: 원하는 결과를 찾을 수 없음)
// 하한이 상한보다 같거나 작으면 반복
Repeat Until (L <= U)
Begin Repeat
// 원하는 결과를 찾음
If (find solution at T) Then
Break
// T에 대한 값이 원하는 값보다 큰 경우 -> 상한을 T보다 1 작은 값으로 변경
If (value at T is greator than solution) Then
// T에 대한 값이 원하는 값보다 작은 경우 -> 하한을 T보다 1 큰 값으로 변경
If (value at T is less than solution) Then
Return Solution
구현1 - 배열에서 원소 검색(반복적 방법)
원소가 비내림차순으로 정렬된 배열에서 바이너리서치 - 반복적 방법
- // 원소가 비내림차순으로 정렬이 되어 있는
- // 크기 n의 배열 Array에서 key가 저장되어 있는 위치를
- // 바이너리서치를 이용하여 리턴
- // key가 없는 경우 -1을 리턴
- int BinarySearchLoop(int Array[], int n, int key)
- {
- int U = n-1;
- int L = 0;
- while (L <= U) {
- int T = (U + L) / 2;
- if (Array[T] == key) return T;
- if (Array[T] > key) U = T - 1;
- else L = T + 1;
- }
- return -1;
- }
구현 2 - 배열에서 원소 검색(재귀적 방법)
원소가 비내림차순으로 정렬된 배열에서 바이너리서치 - 재귀적 방법
- // 원소가 비내림차순으로 정렬이 되어 있는
- // 배열 Array에서 key가 저장되어 있는 위치를
- // 바이너리서치를 이용하여 리턴
- // key가 없는 경우 -1을 리턴
- int BinarySearchRecursive(int Array[], int L, int U, int key)
- {
- if (L > U) return -1;
- int T = (U + L) / 2;
- if (Array[T] == key) return T;
- if (Array[T] < key) return BinarySearchRecursive(Array, L, T-1, key);
- else return BinarySearchRecursive(Array, T+1, H, key);
- }
실수범위에서의 바이너리서치
위에서 정수를 기준으로 바이너리 서치를 하는 방법을 반복적 방법과 재귀적 방법으로 살펴보았는데요 상황에 따라서는 실수범위에 대해서 바이너리서치를 해야할 경우도 발생합니다. 뉴턴메소드(Newton's Method)가 그 예인데요 실수 범위에서 바이너리서치를 하는 경우에는 대체로 오차범위가 주어지고 그 오차범위내에 탐색범위가 들어갈때까지 반복을 하게됩니다.
반복적 방법이든 재귀적 방법이든 바이너리서치를 진행하면서 한 이터레이션이 지날때마다 탐색범위가 반으로 줄어들는 것을 이용하는 겁니다.
예를 들어 오차범위 1e-9 이내에서 답을 구하고 싶으면 low bound와 upper bound의 차이가 1e-9 보다 작아질때까지 반복을 하면 됩니다. 제가 개인적으로 더 추천하는 방법은 그냥 충분히 많이 이터레이션을 하는 것입니다. 무슨말이냐 하면 한 100번 정도 무조건 반복을 하는 겁니다.
이게 지금 무슨말을 하는 거냐!! 라고 생각할 수도 있는데요.. 바이너리서치의 이터레이션을 100번을 반복하면 탑색범위가 1/(2^100)까지 좁혀지게 됩니다. 이 정도 탑색범위라면 1e-9 이내로 들어가지 않을까요?? 뭐 상황에 따라 적잘하게 이터레이션 횐수를 정해주면 됩니다만 제 생각엔 최악의 경우에도 1000번 정도면 충분할것이라 생각합니다.
그렇다면 오차범위 내에 들어갈때까지만 비교하면 될것을 왜 쓸데없이 반복을 하냐라고 물어볼수도 있는데요.. 제가 적당히 큰 횟수만큼 반복하는 것을 권장하는 이유는 오차범위 비교 방법은 실수연산의 특성상(precision error가 생기죠) 오차범위내로 수렴하지 못해 무한루프에 빠질 가능성이 있기 때문입니다.
아래에서 3차 방정식의 해를 바이너리서치를 이용하여 구하는 예를 보겠습니다.
구현 3 - ax^3 + bx^2 + cx + d = 0 의 해를 구함(허용 오차범위 1e-9) - 실수범위 바이너리서치(오차범위)
- // ax^3 + bx^2 + cx + d = 0 의 해를 구합니다.
- // 해는 [-1000000000, 1000000000]에 존재한다고 가정함
- double EPSILON = 1e-9;
- double CubicFunction1(double a, double b, double c, double d)
- {
- double L = -1000000000;
- double U = 1000000000;
- double T = (L + U) / 2;
- while (U - L >= EPSILON) {
- double y = a*T*T*T + b*T*T + c*T + d;
- if (y > 0) U = T;
- else L = T;
- T = (L + U) / 2;
- }
- return T;
- }
구현 4 - ax^3 + bx^2 + cx + d = 0 의 해를 구함(허용 오차범위 1e-9) - 실수범위 바이너리서치(적당히반복)
- // ax^3 + bx^2 + cx + d = 0 의 해를 구합니다.
- // 해는 [-1000000000, 1000000000]에 존재한다고 가정함
- double CubicFunction2(double a, double b, double c, double d)
- {
- double L = -1000000000;
- double U = 1000000000;
- double T = (L + U) / 2;
- for (int i = 0; i < 100; i++) {
- double y = a*T*T*T + b*T*T + c*T + d;
- if (y > 0) U = T;
- else L = T;
- T = (L + U) / 2;
- }
- return T;
- }
문제를 풀어봅시다.
이론만 늘어서는 소용이 없겠죠?? 아는 것을 실전에 써 먹을 수 있는 준비가 되어있어야 진정 내것이라고 말할 수 있습니다.
우리같이 아래 문제를 풀어보아요
직선상에 N개의 행성들이 위치해 있습니다. i 번째 행성은 x[i] 좌표에 있고, m[i] 만큼의 질량을 가지고 있으며, 각각의 행성들은 매우 강한 힘에 의하여 고정되어 있습니다. 모든 행성은 x좌표를 기준으로 비내림차순으로 정렬되어 주어집니다.
질량이 m1, m2인 두 물체 사이의 거리가 d일 때, 두 물체는 서로 F = G * m1 * m2 / d^2 의 힘으로 서로 잡아당기는 만유인력이 작용합니다. (G는 양의 상수이다.) 어떤점 P를 기준으로 만유인력의 벡터합이 0이 되는 P의 위치를 equilibrium Point라고 부릅니다.
N개의 점이 있을 때, N-1개의 Equilibrium Point가 존재합니다. 이러한 Equilibrium Point들을 오름차순으로 정렬하여 소수점이하 9자리까지 출력하시오.
힌트: 각 Equilibrium Point는 이웃한 행성과 행성사이에 하나씩 존재합니다.
풀이보기
EP의 위치를 x'이라 하고 가상의 질량 m'을 부여하면 EP의 왼쪽에 위치한 행성으로부터 받는 중력은 다음과 같습니다.
EP는 중력이 0이 되는 위치이므로 양쪽에서 받는 중력이 같아야 합니다. 따라서 F1 = F2인 x'을 찾아야합니다.
G * m' * ∑ m[k] / (x[i] - x')^2 (k = 0....i) = G * m' * ∑ m[k] / (x[i] - x')^2 (k = i+1....n)
양변의 G * m' 을 소거하면,
∑ m[k] / (x[i] - x')^2 (k = 0....i) = ∑ m[k] / (x[i] - x')^2 (k = i+1....n)
m과 x는 주어지므로 위 식에서 미지항은 x'밖에 없습니다. x'은 뉴턴메소드(바이너리서치)를 이용하여 구할 수 있습니다.
- void EquilibriumPoint(double x[], double m[], int n)
- {
- // n-1개의 Equilibrium Point가 존재함
- for (int i = 0; i < n-1; i++) {
- double L = x[i];
- double U = x[i+1];
- double T = (L + U) / 2;
- // 적당히 큰 횟수 반복(200회 -> 오차범위 1/(2^200))
- for (int j = 0; j < 200; j++) {
- double F1 = 0;
- double F2 = 0;
- // 왼쪽에 위치한 행성의 중력의 합
- for (int k = 0; k <= i; k++)
- F1 += m[k] / pow(x[k] - T, 2.0);
- // 오른쪽에 위치한 행성의 중력의 합
- for (int k = i+1; k < n; k++)
- F2 += m[k] / pow(x[k] - T, 2.0);
- // 왼쪽에서 더 큰 중력을 받음 -> EP는 좀 더 오른쪽에 있다
- if (F1 > F2)
- L = T;
- // 오른쪽에서 더 큰 중력을 받음 -> EP는 좀 더 왼쪽에 있다.
- else
- U = T;
- T = (L + U) / 2;
- }
- printf("%.9f\n", T);
- }
- }
출처: TopCoder - Single Round Match 421
휴.. 이상으로 바이너리서치에 대해서 알아봤는데요.. 왠지 쓰고나니 마지막 문제가 좀 어려웠던게 아닌가 생각이 드네요 ^^;;
다음에는 주제를 약간 벗어나서 C++의 STL(Standard Template Library)에 대해서 포스팅을 해볼까 합니다.
뭐 제가 C++을 주로 사용하다 보니.. C++을 안쓰시는 분들한테는 전혀 도움이 되지 않겠지만 그래도 알아두면 좋겠지요 ㅎㅎ
저번 포스팅에서 예고해드린데로 이번에는 재귀호출에 대해서 다뤄볼까합니다.
물론 멤버십에 계신분들중에 재귀호출을 어려워 하실 분들은 없으리라 생각하는데요, 학교에서 주위를 살펴보면 재귀호출을 잘 못하는 친구나, 후배나, 등등 많은 것 같습니다. 그 만큼 재귀호출이 직관적으로 이해가 잘 안되는 부분인가 봅니다. C++과 싸우다 보면 포인터에서 한 번 좌절을 하게 되고 포인터를 넘고나면 재귀호출이 또다시 태클을 건다는.. 뭐 그런 전설이 내려오는데요.. 저도 지금 재귀호출을 어떻게 다뤄야할지 막막합니다 ㅠㅠ
뭐.. 어쨌든..... 각설하고 시작하겠습니다.
재귀(Recursion)
주어진 문제를 재귀적으로 푼다는 말은 문제의 답이 그 문제와 동일한 형태의 더 작은 부분문제(sub problem)의 답에 의존적(dependency)이다 라는 의미를 가지고 있습니다.
흠.. 무슨말인지 모르겠습니다. 이해를 돕기 위해 쉬운 예를 들어 보겠습니다.
누가 저 작품에 레고블럭이 몇 개가 쓰였는지 물어봅니다.
도저히 한눈에 레보블럭이 몇 개가 쓰였는지 알지 못하겠습니다.
레고를 쪼갭니다.
아직 각각이 몇개씩인지 모르겠습니다.
다시 레고를 쪼갭니다.
아직 모르겠습니다.
다시 레고를 쪼갭니다.
...
...
이제 몇 개인지 눈에 보입니다.
쪼갰던 레고를 합칩니다.
각각의 답도 같이 합칩니다.
쪼갰던 다른 레고를 합칩니다.
각각의 답도 같이 합칩니다.
계속 합칩니다.
...
처음의 레고 작품으로 돌아왔습니다.
이제 이 작품에 레고블럭이 몇 개가 쓰였는지 압니다.
위의 과정을 분할정복(Divide and Conquer)라고 합니다.
재귀호출은 분할정복, 백트레킹 뭐 이런 녀석들이랑 땔래야 땔 수 없는 사이인데요, 이 녀석들의 특징이 주어진 문제를 더 작은 문제로 분할하여 문제를 해결한다는 점에서 동일한 특성을 가지고 있기때문입니다. 실제로 거의 대부분의 경우 D&C나 백트레킹은 재귀함수로 구현하는 경우가 많습니다.
재귀함수(Recursive Function)
재귀적으로 문제를 푸는 함수를 재귀함수라고 하고 직간접적으로 자기자신을 호출합니다.
재귀적으로 문제를 푼다(동일한 형태의 다 작은 부분문제를 풀어나감)는 것을 생각해 봤을 때, 반복이 진행될 때마다 동일한 작업을 해야 한다는 것을 짐작할 수 있습니다.(동일한 형태의 문제를 푸니깐;) 그리고 더 이상 문제를 쪼개지 않아도 되는 상황에 언젠가는 도달해야 합니다. 따라서 재귀함수는 자기자신을 호출하고(동일한 형태) 언젠가는 종료를 해야합니다.
또.. 무슨 말인지 모르겠습니다. 프로그래머는 코드로 말한다고 코드를 보는게 더 쉽겠네요
수도코드보기
Begin
If It can possible to solve this problem then
Solve problem
Return solution
Else
Divide problem to subproblem1 and subproblem2
// 쪼갠 문제를 가지고 재귀호출 ㄱㄱㅆ
Type res2 = RecursiveFunction(subproblem2)
// 쪼개진 문제의 답을 조합하여 이 문제의 답을 구해 리턴
Return compose res1 and res2
현실적인 예를 들기위해 n!을 재귀적으로 구해보도록 합시다.
여러분은 10!이 얼마인지 아십니까?? 모르겠죠?? 저도 모릅니다. 그래도 10! 은 9!에다가 10을 곱했다는 거는 알 것 같습니다.. 모르시면 중학교 수학책을 찾아보십시오.
코딩을 하기 위해서는 수식을 일반화할 필요가 있는데요 지금껀 일반화하기 그닥 어렵지 않습니다.
= (n-1) * n (n >= 2) - 재귀호출
위와 같은 식을 점화식(Recurrence relation)이라고 합니다. 고등학교 수학시간에 수열의 일반항을 구할때 많이 들었던 용어일겁니다. 각설하고 점화식을 알았으면 바로 그래도 코드로 옮겨주면 됩니다.
- int fac(int n)
- {
- if (n <= 1) return 1;
- return n * fac(n-1);
- }
제가 주로 사용하는 언어가 C++인 관계로 C++로 코딩했습니다. 뭐 근데 생각해보니 저 함수는 자바나 C#으로 짜도 저렇게 나오겠네요 쿨럭; 여튼 앞으로도 계속 C++로 작성하겠습니다.
호출이 일어나는 순서를 도식화 하면 더 알기 쉽겠죠?
fac(5)를 호출했을 때 상태의 변화를 도식화하면 아래와 같습니다.
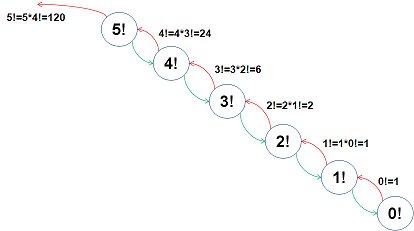
뭐 여기까지 이미 다 알고계신 내용이었을테구요..
재귀함수를 작성하다 보면 의도하지 않은 크리티컬한 문제에 봉착하게 되는 경우가 있습니다. 아래의 예를 봅시다.
공대를 다니면서 절대 피할수 없는 수열이 있습니다. 바로 피보나치수열인데요. 점화식은 아래와 같습니다.

점화식대로 재귀함수를 코딩하면 이렇게 나오죠
- int fib(int n)
- {
- if (n <= 1) return n;
- return fib(n-1) + fib(n-2);
- }
그런데 여기에 엄청난 문제가 있습니다.. 눈치 채셨습니까??
함수의 콜 상태를 도식화 해보면 이렇습니다.
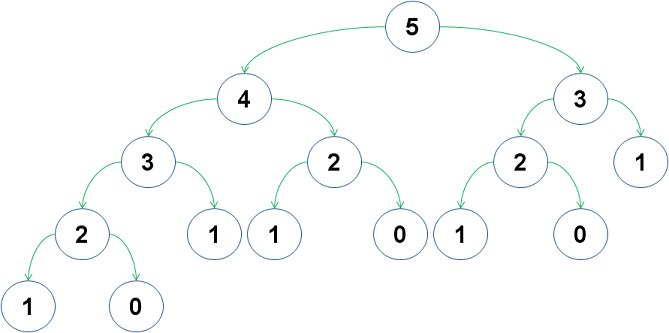
이 엄청난 문제 눈치채셧습니까??
그림을 잘 보면 fib(3)이 두번 계산 되는걸 알 수 있습니다. fib(2)는 3번이구요 fib(1)은 5번이나 호출되네요..
저게 fib(5)를 구하는 그림이라 그렇지 fib(50)을 구한다고 생각해보십시오.. 끔찍합니다..
분석을 해보면 저런식으로 함수를 구현하게 되면 fib(n)을 구하는데 대략 2^n번의 함수 호출이 발생합니다. fib(50)을 구한다면??또 이 표현 안할수가 없네요. 지구가 멸망할때까지 답을 못봅니다
다행이도 이런 문제를 해결하는 Memoization이라는 기법(Memorization이 아닙니다)이 있는데요, 언젠가 포스팅을 하겠습니다.
하노이의 탑
마지막으로 하노이 탑을 옮겨보도록 하겠습니다.
하노이의 탑 하러가기
하노이의 탑은 세개의 공간 중 한 공간에 쌓여진 탑을 한 번에 하나의 층만 이동하여 다른 공간으로 이동하는 문제인데요 이동하는 도중에 크기가 더 큰 층이 작은 층 위에 올라올 수 없습니다.
최소의 횟수로 하노이의 탑을 옮기는 방법은 단 한가지가 존재하는데 옮기는 횟수가 무려 2^n-1 번이나 됩니다.
인도의 베레니스에 있는 한 사원에 64층의 하노이 탑이 있는데 이 탑을 위의 규칙에따라 옮기면 탑은 무너지고 세상은 종말한다라는 예언이 전해오는데요.. 사실 64층의 탑을 사람의 힘으로 옮기려면 영겁의 세월이 걸립니다. 그 전에 세상이 종말하겠죠;
그럼 본격적으로 하노이 탑을 옮겨보도록 하겠습니다.
source(S)에 있는 n층의 하노이탑을 destination(D)으로 옮기고자 합니다. 그리고 이를 위해 temp(T)라는 공간이 준비되어 있습니다.
크게 생각해보면 n층의 하노이 탑을 옮기려면 n-1층까지 모든 블록을 S->T로 옮기고 젤 마지막 조각을 S->D로 옮긴 다음에 T에 있는 n-1층의 하노이탑을 D위에 쌓으면 됩니다. 그럼 여기에서 n-1층의 하노이 탑을 옮기는 과정(S->T, T->D)이 필요한데, 이 과정은 n층의 하노이 탑을 옮기는 과정과 방법이 같습니다.
우선 n-1층의 탑을 S->T로 옮기는 것을 생각해봅시다. 이경우 S가 원본이되고 T가 목적지가 됩니다. 각각 S'과 D'이라고 하고 남은 슬롯인 D를 이 경우에서는 임시공간으로 사용하므로 T'이라하면, 우선 n-2층까지 S'->T'으로 옮기고 n-1층을 S'->D'으로 옮깁니다. 그 후 T'에 있는 n-2층까지의 블록을 D'위로 옮겨놓으면 됩니다. 여기에서 또 n-2층을 옮기는 방법을 알아야 하는데요 n-1층을 옮기는 방법과 똑같이 하면 됩니다. 이 과정을 1층이 될때까지 재귀적으로 수행하면 됩니다.
그림보기
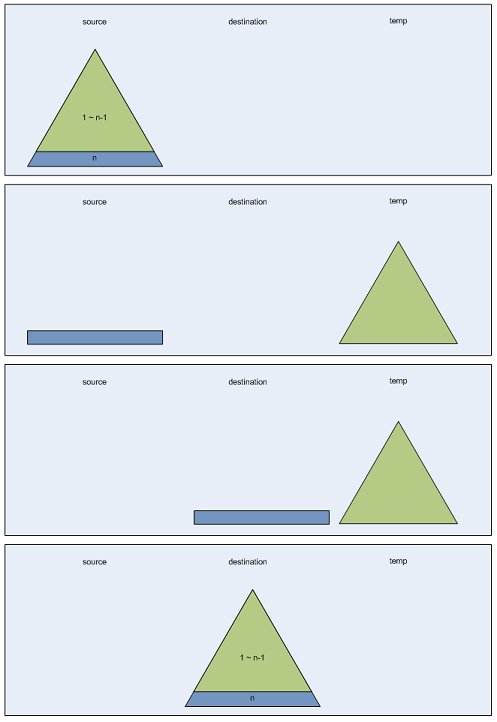
이제 위의 과정을 함수로 작성해봅시다.
함수 TowerOfHanoi(int n, int a, int b, int c) 을 n층의 하노이이 탑을 a에서 b로 c의 임시공간을 이용해서 옮기는 함수라고 정의하면 함수의 몸체는 위에서 설명한 세단계(n-1층까지 a->c로 옮김, n층을 a->b로 옮김, n-1층까지 c->b로 옮김)으로 구성됩니다. 이 세 단계를 모두 재귀호출을 이용하여 구현하면 하노이의 탑은 아래와 같이 간단하게 구현됩니다.
- // 하노이의 탑
- // n층의 탑을 a에서 b로 옮긴다. c는 여유공간
- void TowerOfHanoi(int n, int a, int b, int c)
- {
- // 종료조건
- if (n == 1)
- {
- printf("%d -> %d\n", a, b);
- return;
- }
- // 1~n-1층까지 a->c로 옮긴다
- TowerOfHanoi(n-1, a, c, b);
- // n번째 층을 a->b로 옮긴다
- TowerOfHanoi(1, a, b, c);
- // 1~n-1층까지 c->b로 옮긴다
- TowerOfHanoi(n-1, c, b, a);
- }
TowerOfHanoi(4, 1, 2, 3); 을 실행한 결과는 다음과 같습니다.
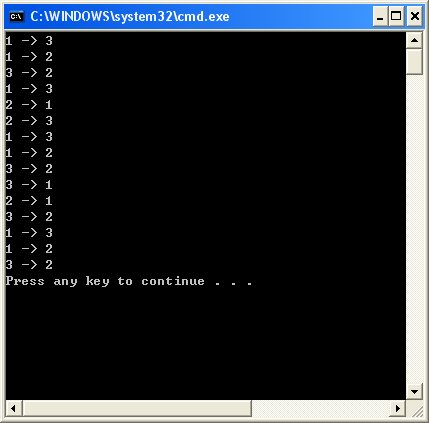
답이 제대로 나온 것 같나요??
다음에는 바이너리서치를 구현하는 방법에 대해서 얘기해보겠습니다.
안녕하세요.
이번에는 지난 포스팅에 이어 알고리즘의 차수에 대해서 알아보겠습니다.
지난글의 마지막에 이번시간부터는 본격적으로 코딩기법에 대해서 포스팅하겠다고 했는데 생각을 해보니 일단 차수에 대해서는 언급을 하고 넘어가야 할 것 같아서 순서를 바꿨습니다 ^^
알고리즘의 분석
알고리즘이 문제를 얼마나 효과적으로 해결하는지를 결정하기 위하여 알고리즘을 분석할 필요가 있습니다. '알고리즘 코딩기법 1 - Introduction' 에서 소개했던 순차검색과 이분검색의 비교가 바로 알고리즘의 분석이라고 할 수 있고 분석결과 n이 커질수록 이분검색이 유리하다고 결론을 내렸었는데요, 이번 파트에서는 알고리즘의 분석에 대해서 좀 더 자세히 알아보겠습니다.
복잡도 분석(complexity analysis)
시간을 기준으로 알고리즘의 효율을 분석할 때 보통은 CPU에서의 실제 작동시간으로 분석을 하지는 않습니다. 왜냐하면 사용하는 컴퓨터의 성능에 따라 결과가 다르게 나타나기 때문입니다. 그 외에 알고리즘을 구현하는데 사용한 언어나 컴파일러, OS에 따라서도 시간이 다르게 측정될 수 있습니다. 따라서 알고리즘의 효율성을 분석하기 위해서는 위에서 언급한 것들과는 독립된 다른 기준이 필요합니다.
알고리즘의 시간복잡도를 분석할 땐 '1-Introduction' 에서 그랬듯이 입력크기 n에 대해서 알고리즘의 단위연산이 수행되는 횟수를 비교하여 분석하는 기법을 가장 많이 사용합니다. 일반적으로 알고리즘의 실행시간은 입력의 크기에 따라 증가하고, 총 실행시간은 단위연산이 몇 번 수행 되는가에 비례합니다. 따라서 단위연산이 수행되는 횟수를 입력의 크기에 대한 함수로 나타내어 알고리즘의 효율성을 분석할 수 있습니다.
입력크기(input size)
말 그대로 알고리즘으로의 입력의 크기를 의미합니다. 대부분의 알고리즘에서 입력을 크기를 구하기는 매우 쉽습니다. 예를 들어 n개의 아이템을 정렬하는 알고리즘에서 입력크기는 아이템의 갯수인 n이 됩니다. n번째 피보나치항을 구해야 하는 알고리즘의 시간복잡도는 n에 비례할 것입니다. (하지만 엄밀히 따지면 입력크기가 n이라고 말할 수는 없습니다)
단위연산(basic operation)
어떤 명령문이나 일련의 명령문의 집합을 선정하여, 알고리즘이 수행한 총 작업의 양을 이 명령문이나 명령문의 집합을 수행한 횟수에 대략적으로 비례하게 되었을 때, 이 것을 단위연산이라고 합니다. 예를 들어 버블소트 알고리즘에선 두 아이템을 비교를 하고 아이템을 위치를 바꾸는 작업을 하나의 단위연산으로 볼 수 있습니다.
시간복잡도 분석(time complexity analysis)
알고리즘의 시간복잡도 분석은 입력크기의 값에 대해서 단위연산을 몇 번 수행하는지를 구하는 것입니다.
차수
동일한 일을 하는 두 개의 알고리즘이 있습니다. 하나는 시간복잡도가 100n이고 나머지 하나는 0.01n^2 일 때, 어떤 알고리즘이 더 효율적일까요..
사실 두 알고리즘 중 어떤 알고리즘을 선택해야 하는지는 부등식으로 쉽게 풀 수 있습니다. 아래의 부등식을 봅시다.
100n < 0.01n^2
부등식을 풀면 n > 10,000 이 됩니다. 해석해보면 n이 1만 이상일때 두 번째 알고리즘의 시간복잡도가 더 크다(더 느리다)라는 말이 됩니다. 따라서 n이 1만 이하일 때는 두번째 알고리즘을 선택하고 이상일 때는 첫번째 알고리즘을 선택하는 것이 유리합니다.
궁극적으로는 100n의 시간복잡도를 가진 첫번째 알고리즘이 더 효율적인 알고리즘이 됩니다. 왜나하면 입력크기가 어떤 임계값을 넘으면 그 후로는 항상 첫번째 알고리즘이 효율적이기 때문입니다.
위의 예에서 100n과 같은 시간복잡도를 가진 알고리즘을 1차시간 알고리즘(linear-time algorithms)이라고 하고 0.01n^2과 같은 시간복잡도를 가진 알고리즘을 2차시간 알고리즘(quadratic-time algorithm)이라고 힙니다. 궁극적으로는 어떤 1차시간 알고리즘도 어떤 2차시간 알고리즘보다 항상 효율적입니다.
이해를 돕기위해 시간복잡도가 아래와 같은 세 개의 알고리즘을 살펴봅시다.
algorithm2의 시간복잡도: 0.1n^2
algorithm3의 시간복잡도: 0.1n^2 + n + 100
n이 커짐에 따라 각 알고리즘의 단위연산 수행횟수를 살펴보면 다음과 같습니다.
| n | algorithm1(n) | algorithm(0.1n2) | algorithm3(0.1n2+n+100) |
| 10 | 10 | 10 | 120 |
| 20 | 20 | 40 | 160 |
| 50 | 50 | 250 | 400 |
| 100 | 100 | 1,000 | 1,200 |
| 1,000 | 1,000 | 100,000 | 101,100 |
표에서 볼 수 있듯이 n이 커지면 커질수록 시간복잡도는 시간복잡도 함수의 최고차항의 영향을 가장 크게 받는다는 것을 알 수 있습니다. 즉 다른 항들의 값은 최고차항의 값에 비해 궁극적으로 대수롭게 되기 때문에 알고리즘의 효율성을 비교할 때는 보통 최고차항의 차수를 봅니다.
가장 흔하게 나타나는 복잡도 카테고리와 그래프를 보시겠습니다.
| θ(lg n) < θ(n) < θ(n lg n) < θ(n2) < θ(n3) < θ(2n) < θ(n!) |
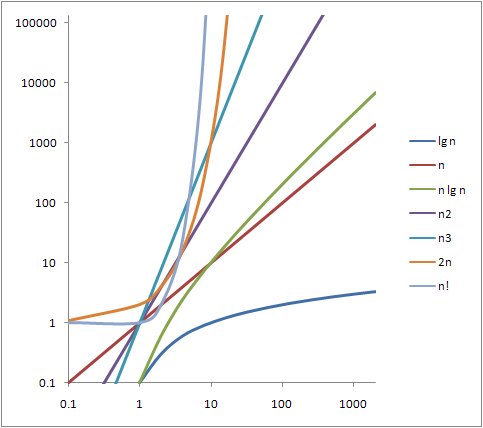
주어진 시간복잡도에 대한 알고리즘의 실행시간은 대략 아래의 표와 같은 비율을 나타냅니다.
| n | lg n | n | n lg n | n2 | n3 | 2n | n! |
| 10 | 0.003 μs | 0.01 μs | 0.033 μs | 0.10 μs | 1.0 μs | 1 μs | 10.87 ms |
| 20 | 0.004 μs | 0.02 μs | 0.086 μs | 0.40 μs | 8.0 μs | 1 ms | 23 years |
| 30 | 0.005 μs | 0.03 μs | 0.147 μs | 0.90 μs | 27.0 μs | 1 s | 2.5 x 1016 years |
| 40 | 0.005 μs | 0.04 μs | 0.213 μs | 1.60 μs | 64.0 μs | 18.3 min | |
| 50 | 0.006 μs | 0.05 μs | 0.282 μs | 2.50 μs | 125.0 μs | 13 days | |
| 102 | 0.007 μs | 0.10 μs | 0.664 μs | 10.00 μs | 1.0 ms | 4 x 1013 years | |
| 103 | 0.010 μs | 1.00 μs | 9.966 μs | 1.00 ms | 1.0 s | ||
| 104 | 0.013 μs | 10.00 μs | 130.000 μs | 100.00 ms | 16.7 min | ||
| 105 | 0.017 μs | 0.10 ms | 1.670 ms | 10.00 s | 11.6 days | ||
| 106 | 0.020 μs | 1.00 ms | 19.930 ms | 16.70 min | 31.7 years | ||
| 107 | 0.023 μs | 0.01 s | 0.222 s | 1.16 days | 31709 years | ||
| 108 | 0.027 μs | 0.10 s | 2.660 s | 115.70 days | 3.17 x 107 years | ||
| 109 | 0.030 μs | 1.00 s | 29.900 s | 31.70 years |
표에서 알 수 있듯이 차수가 올라갈수록 입력 크기가 증가함에 따라 알고리즘의 수행시간은 기하급수적으로 오래걸린다는 것을 알 수 있습니다. 알고리즘의 선택이 중요한 이유가 여기에 있습니다. 10억개의 아이템을 정렬해야 하는데 버블정렬을 사용했다면 31년이나 걸렸겠지만 다행히 O(n log n)에 정렬을 하는 알고리즘이 존재하기 때문에 그 알고리즘을 선택을 하면 29.9초만에 정렬을 완료 할 수 있습니다.
만약 어떤 문제를 해결하는데 2^n의 시간복잡도를 가지는 알고리즘은 금방 생각해 낼 수 있는데 입력크기가 1000이라면 어떨까요? 아마 우주가 멸망할때까지 2^n의 알고리즘으로는 문제의 답을 볼 수 없을것입니다. 이럴때에는 더 좋은 알고리즘(차수가 n^3이하인 알고리즘)을 찾아보거나 최적화알고리즘을 선택해야 합니다.
이상으로 알고리즘의 차수와 효율적인 알고리즘의 선택이 중요한 이유에 대해서 간략히(??) 살펴보았습니다.
Big-O 표기법에 대해서도 살펴보려 했으나 수식이 좀 들어가는 관계로 생략하겠습니다. 혹시나(설마??) 요청이 있다면 다음 기회에 Big-O 표기법에 대해서도 다뤄보겠습니다.
그리고 지금까지는 알고리즘의 효율성을 분석하면서 시간복잡도에 대해서만 고려했는데 메모리가 제약적인 임베디드시스템 같은 경우에는 시간복잡도보다 공간복잡도를 더 중요하게 다뤄야 할 상황도 있습니다. 하지만 대부분의 경우에 메모리가 훨씬더 싸고 공간복잡도는 시간복잡도만큼이나 기하급수적으로 증가하지 않기 때문에(알고리즘의 선택에 따라 공간복잡도도 엄청난 차이를 보이지만 시간복잡도에 비하면 새발의 피라고 표현하고 싶네요) 생략하겠습니다.
지난번에 이어 이번 포스팅까지 머리아픈 글로만 채워진 지루한 포스팅이었는데요..
다음 포스팅에는 정말로 시그 주제에 맞게끔 코딩주제로 넘어가 제귀호출의 코딩과 그 동작원리에 대해서 살펴보도록 하겠습니다.
참고: Foundations of Algorithms / Richrd E. Neapolitan


